

Kvadratna funkcija spremenljivke x je funkcija 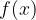 , v kateri spremenljivka x nastopa pod kvadratom. Najbolj osnovna kvadratna funkcija je:
, v kateri spremenljivka x nastopa pod kvadratom. Najbolj osnovna kvadratna funkcija je:
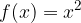
Običajno pa je členu z 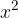 prištet še člen z
prištet še člen z 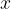 in kakšno število.
in kakšno število.
Graf kvadratne funkcije imenujemo parabola in jo prepoznamo po čašasti obliki:
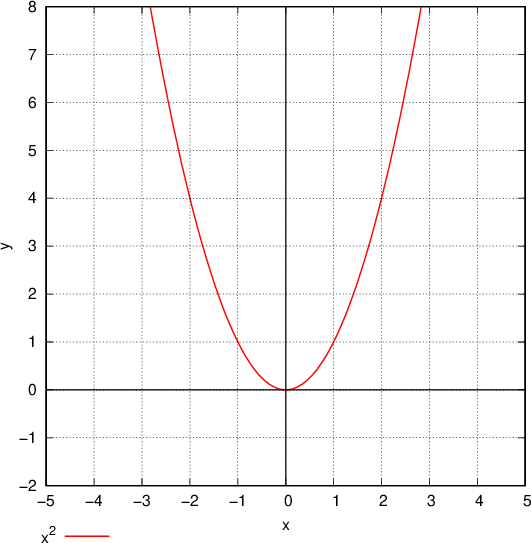
Enačbo funkcije lahko zapišemo v več oblikah, pri čemer lahko iz vsake oblike določimo kakšno lastnost funkcije.
Kvadratna funkcija je realna funkcija s predpisom v tako imenovani splošni obliki:
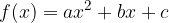
kjer so koeficienti a, b in c poljubna realna števila. Koeficient a imenujemo koeficient kvadratnega člena ali vodilni koeficient, b koeficient linearnega člena in c stalni, svobodni, prosti, ali konstantni člen.
Koeficient a ne more biti enak 0, ker potem funkcija ni več kvadratna.
Obliko parabole določa vodilni koeficient a:
Če je vodilni koeficient a > 0 je parabola obrnjena "navzgor" in ima obliko:
Če je vodilno koeficient a < 0 je parabola obrnjena "navzdol" in ima obliko:
Širina parabole je odvisna od absolutne vrednosti vodilnega koeficienta 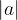 . Večja je absolutna vrednost, ožja in bolj strma je parabola:
. Večja je absolutna vrednost, ožja in bolj strma je parabola:
Splošno obliko kvadratne funkcije 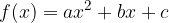 zapišemo v ničelni obliki s pomočjo zapisa:
zapišemo v ničelni obliki s pomočjo zapisa:
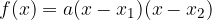
kjer so:
a koeficient kvadratnega člena ali vodilni koeficient in
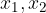 ničli kvadratne funkcije.
ničli kvadratne funkcije.
Ničli kvadratne funkcije izračunamo po obrazcu:
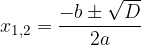
kjer je D diskriminanta, ki jo izračunamo po obrazcu:
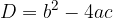
Ničle funkcije so tista števila x, pri katerih je vrednost funkcije f(x) enaka 0. Ničle nam povedo, kje funkcija seka os x. Pri tem je število in značaj ničel kvadratne funkcije je odvisen od diskriminante D.
Poglejmo, kako so ničle kvadratne funkcije odvisne od diskriminante D:
Če je D > 0, ima parabola dve različni realni ničli 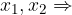 parabola seka os x, se pravi ima lahko eno izmed naslednjih oblik:
parabola seka os x, se pravi ima lahko eno izmed naslednjih oblik:
Če je D = 0, ima parabola eno samo dvojno realno ničlo 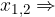 parabola se dotika osi x, se pravi ima lahko eno izmed naslednjih oblik:
parabola se dotika osi x, se pravi ima lahko eno izmed naslednjih oblik:
Če je D < 0, parabola nima ničel  parabola ne seka in se ne dotika osi x, se pravi ima lahko eno izmed naslednjih oblik:
parabola ne seka in se ne dotika osi x, se pravi ima lahko eno izmed naslednjih oblik:
Splošno obliko kvadratne funkcije: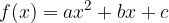 zapišemo v temenski obliki s pomočjo zapisa:
zapišemo v temenski obliki s pomočjo zapisa:
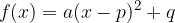
kjer so:
a koeficient kvadratnega člena ali vodilni koeficient in
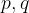 koordinati temena parabole T(p, q).
koordinati temena parabole T(p, q).
Koordinati temena izračunamo z enačbama:
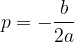
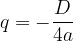
kjer je D diskriminanta, ki jo izračunamo po obrazcu:
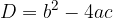
Teme krivulje T(p, q) je v ravninski geometriji točka, kjer doseže ukrivljenost krivulje ekstremno (minimalno ali maksimalno) vrednost.
Poglejmo si geometrijski pomen temena:
Če je a > 0 je parabola obrnjena navzgor, torej ima v temenu T(p, q) pri p najmanjšo vrednost q:
Če je a < 0 je parabola obrnjena navzdol, torej ima v temenu T(p, q) pri p največjo vrednost q:
Iz gornjih grafov razberemo, da je simetrijska os parabole paralelna z ordinatno osjo in je njena enačba:
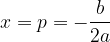
Do temenske oblike kvadratne funkcije lahko pridemo tudi, če splošno obliko dopolnimo do popolnega kvadrata.
Izpeljimo temensko obliko kvadratne funkcije s popolnitvijo do popolnega kvadrata:
Dobili smo temensko obliko kvadratne funkcije.
Pri risanju parabole 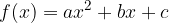 , ki je podana v splošni obliki, si pomagamo s ključnimi točkami, ki so:
, ki je podana v splošni obliki, si pomagamo s ključnimi točkami, ki so:
ničle kvadratne funkcije
Ničle so točke, kjer funkcija seka, oziroma se dotika x osi in zanje velja y = 0:
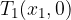
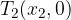
začetna vrednost funkcije
Začetna vrednost funkcije je točka, v kateri funkcija seka os y in zanjo velja x = 0:
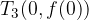
teme funkcije
Teme je točka, kjer ima kvadratna funkcija ekstremno (minimalno ali maksimalno) vrednost:
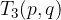
zrcalna slika začetne vrednosti
Ker je kvadratna funkcija simetrična glede na navpičnico skozi teme lahko kot dodatno oporno točko uporabimo še točko, ki je zrcalna slika začetne vrednosti:
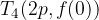
V koordinatni sistem vrišemo izračunane ključne točke in skoznje narišemo graf podane kvadratne funkcije. Obrazci za izračun ključnih točk so:
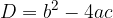
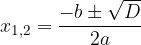
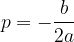
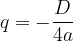
Iz funkcije 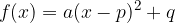 , ki je podana v temenski obliki, razberemo naslednja, za risanje njenega grafa, pomembna podatka:
, ki je podana v temenski obliki, razberemo naslednja, za risanje njenega grafa, pomembna podatka:
izhodiščno funkcijo 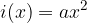 in
in
teme T(p, q).
Najprej narišemo izhodiščno funkcijo 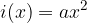 , ki je najpreprosta oblika kvadratne funkcije (ker sta b = 0 in c = 0) in jo zato lahko narišemo kar s pomočjo tabeliranja. Za x-e izberemo poljubne vrednosti (običajno
, ki je najpreprosta oblika kvadratne funkcije (ker sta b = 0 in c = 0) in jo zato lahko narišemo kar s pomočjo tabeliranja. Za x-e izberemo poljubne vrednosti (običajno 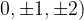 in izračunamo pripadajoče funkcijske vrednosti. S tem dobimo točke skozi katere gre funkcija.
in izračunamo pripadajoče funkcijske vrednosti. S tem dobimo točke skozi katere gre funkcija.
V koordinatni sistem vrišemo dobljene točke in skoznje potegnemo izhodiščno funkcijo 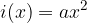 .
.
Funkcijo 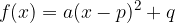 potem narišemo tako, da narisani izhodiščni graf
potem narišemo tako, da narisani izhodiščni graf 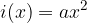 togo premaknemo tako, da je njeno teme v točki T(p, q), ki je teme podane funkcije.
togo premaknemo tako, da je njeno teme v točki T(p, q), ki je teme podane funkcije.
Medsebojno lego med parabola 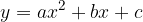 in premica
in premica 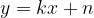 določimo tako, da rešimo sistem njunih enačb:
določimo tako, da rešimo sistem njunih enačb:
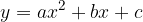
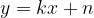
Razrešimo ga z zamenjalnim načinom. V prvi enačbi neznanko y nadomestili z izrazom v drugi enačbi:
Abscisa presečišča parabole in premice je rešitev kvadratne enačbe:
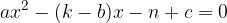
ki ima koeficiente:
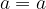
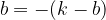
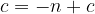
Medsebojna lega parabole in premice je odvisna od diskriminante D, ki jo izračunamo po obrazcu:
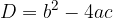
Diskriminanta na lego med kvadratno funkcijo in enačbo vpliva tako:
Če je D > 0, premica seka parabolo v dveh točkah
Če je D = 0, se premica dotika parabole, se pravi, da je njena tangenta
Če je D < 0, premica in parabola nimata nobene skupne točke