Prijava z e-naslovom
Prijava brez gesla
Absolutna vrednost nekega realnega števila je v matematiki elementarna funkcija, ki predstavlja njegovo oddaljenost od številskega izhodišča (točke 0) na številski premici.
Absolutno vrednost števila a po navadi označimo z navpičnim oklepajem :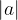 
Vemo, da oddaljenost od koordinatnega izhodišča ni nikoli negativna, torej je absolutna vrednost poljubnega števila vedno nenegativno število.
Za absolutno vrednost torej velja:
absolutna vrednost pozitivnega števila je enaka danemu številu
absolutna vrednost negativnega števila je enaka nasprotnemu številu danega števila
absolutna vrednost števila 0 je enaka 0
Matematično lahko to zapišemo kot:
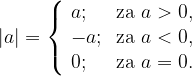
Naj bosta a in b poljubni realni števili. Tedaj veljata naslednji pravili:
velja natanko takrat, ko je
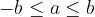
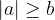velja natanko takrat, ko je
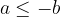
ali
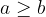
Absolutna vrednost ima v realnem prostoru naslednje lastnosti:
Absolutna vrednost števila a je pozitivna ali enaka 0:
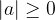
Absolutna vrednost je enaka 0 natanko tedaj, ko je a=0:
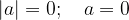
Točki a in -a sta enako oddaljeni od koordinatnega izhodišča, zato je njuna absolutna vrednost enak. Enakost sledi neposredno iz definicije absolutne vrednosti:
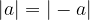
Absolutna vrednost produkta je enaka produktu absolutnih vrednosti:
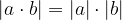
Absolutna vrednost kvocienta je enaka kvocientu absolutnih vrednosti.
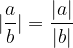
Absolutna vrednost vsote je manjša ali enaka vsoti absolutnih vrednosti. To lastnost imenujemo trikotniška neenakost:
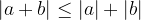
Posledično velja tudi:
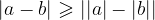
Absolutna vrednost ima dva pomembna pomena v geometriji:
Na številski premici je |a| oddaljenost točke a od izhodišča koordinatnega sistema.
Grafično to prikažemo kot:
ali
S pomočjo absolutne vrednosti lahko izračunamo razdaljo med točkama a in b. Posebnost pri absolutni vrednosti je, da ne rabimo najprej določiti katero število je večje od drugega (vemo: absolutna vrednost poljubnega števila je vedno nenegativno število.) Torej velja:
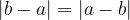
Matematično to zapišemo kot:
Razdalja med točkama a in b je enaka :
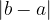
Grafično to prikažemo kot:
