Osebne zbirke


Zaporedje je aritmetično, če je razlika dveh zaporednih členov konstantna oz. ko vsak naslednji člen zaporedja izračunamo tako, da prejšnjemu prištejemo isto število.
Zapišimo nekaj zaporednih členov aritmetičnega zaporedja, pri čemer razliko dveh zaporednih členov označimo z d, prvi člen zaporedja pa z 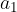 .
.
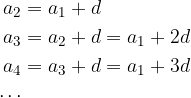
Zapišimo obrazec za splošni člen aritmetičnega zaporedja:
Obrazec za splošni člen aritmetičnega zaporedja, kjer je 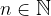 , je:
, je:
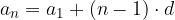
Velja, da je splošni člen aritmetičnega zaporedja linearna funkcija spremenljivke n.
Razliko dveh zaporednih členov imenujemo diferenca aritmetičnega zaporedja, označimo jo z d. Diferenca je vedno konstantna.
Obrazec za diferenco aritmetičnega zaporedja, kjer je 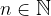 , je:
, je:
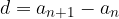
oziroma
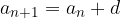
Naraščanje in padanje aritmetičnega zaporedja je odvisno od diference zaporedja.
Velja:
če je 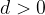 , potem je zaporedje naraščajoče
, potem je zaporedje naraščajoče
če je 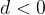 , potem je zaporedje padajoče
, potem je zaporedje padajoče
če je 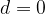 , potem je zaporedje konstantno
, potem je zaporedje konstantno
Vsak člen aritmetičnega zaporedja, z izjemo prvega, je enak aritmetični sredini svojih sosedov.
Aritmetična sredina poljubnih dveh števil a in b je število:
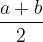
Aritmetična sredina dveh poljubnih simetrično ležečih členov zaporedja pa je člen:
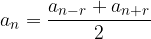
Imejmo števili a in b in denimo, da želimo med ti dve števili vriniti m števil tako, da števila 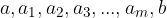 tvorijo aritmetično zaporedje. Ta postopek imenujemo linerna interpolacija.
tvorijo aritmetično zaporedje. Ta postopek imenujemo linerna interpolacija.
Z linearno interpolacijo dobimo aritmetično zaporedje, za katero velja, da je sestavljeno iz 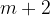 členov, prvi člen
členov, prvi člen 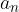 je enak a in zadnji člen
je enak a in zadnji člen 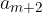 je enak b.
je enak b.
Poiščimo obrazec za izračun diference tako dobljenega aritmetičnega zaporedja:
Obrazec za diferenco aritmetičnega zaporedja, ki ga dobimo z linearno interpolacijo, ko med števili a in b vrinemo m števil, je: