Osebne zbirke


V snovi delujejo medmolekularne ali medatomske sile. To so privlačne sile. Dejansko so to kemijske vezi med molekulami in atomi. Velikost take sila deloča agregatno stanje:
močne medatomske in medmolekularne sile naredijo snov trdno.
"srednje močne" sile vladajo v kapljevinah;
šibke sile pa vladajo v plinu.
Medmolekularne sile so v osnovi električne sile (glej Sile v električnem polju. Coulombov zakon). Kako velike so, je odvisno od same snovi, v kakšnem agregatnem stanju je snov (trdna, kapljevinasta, plinasta), kako je kristalizirana in tudi od temperature snovi.
Kolikšne so sile v snovi lahko raziskujemo tako, da na snov delujemo z zunanjo silo. Zunanja sila snov deformira. Razdalje med molekulami se večajo ali manjšajo - odvisno od smeri zunanje sile.
Kako se spreminja razdalja med atomi ali molekulami v odvisnosti od zunanje sile kaže graf na sliki 1 levo. Slika 1 desno predstavlja model atomov, na katere deluje zunanja sila. (Podobno bi veljalo tudi za molekule). Temnejši del na sliki je jedro atoma, svetlejši pa elektronski plašč okoli jedra. Če je snov trdna (ali pa tudi kapljevinasta), se atomi vedno dotikajo, le pri plinih so lahko razmaknjeni.
Pod vplivom zunanje sile se stiskajo ali natezajo, zato se razdalja r med njimi spreminja:
Točka F = 0
Če ni zunanje sile, je razdalja med atomi (molekulami) približno enaka 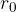 . Atome si predstavljajmo v tem primeru kot krogce z radijem
. Atome si predstavljajmo v tem primeru kot krogce z radijem 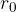 - slika 1 sredina desno.
- slika 1 sredina desno.
Neposredna okolica F = 0
V ozkem področju v okolici F = 0 velja linearna odvisnost sile od razdalje med molekulami, kar zapišemo kot:
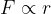
Območje F > 0
Pozitivna zunanja sila stiska molekule - slika 1 zgoraj desno. V trdnini stiskanje močno ovira elektronski plašč okoli jedra atoma. Elektroni so negativno nabiti delci, med katerimi delujejo močne odbojne električne sile (glej Sile v električnem polju. Coulombov zakon). Da bi približali dva atoma, moramo z močno pozitivno zunanjo silo izničiti odbojni vpliv električnih sil.
Območje F < 0
Negativna zunanja sila snov nateza - slika 1 spodaj desno. Natezanju nasprotujejo privlačne sile med molekulami in atomi - kemične vezi. Posledica natezanja zunanje sile je, da se molekule razmikajo - razdalja r med njimi se veča. Pri majhnih silah se razmiki linearno večajo s silo, kasneje pa ne več. Odvisnost sile od razmika postane nelinearna.
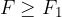
Ko zunanja sila doseže vrednost 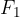 in je razmik med molekulami enak
in je razmik med molekulami enak 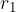 medmolekularna sila pričenja popuščati. Material se pričenja trgati in medmolekularna sila hitro pade na nič.
medmolekularna sila pričenja popuščati. Material se pričenja trgati in medmolekularna sila hitro pade na nič.
Sila lahko deluje na telo v eni sami točki, to je v prijemlišču sile. Običajno sila ne deluje točkasto, pač pa je razporejena po določeni ploskvi. Čim manjša je ploskev, na katero deluje sila, večji je vpliv sile na deformacijo telesa. Pravimo, da je večji tlak sile.
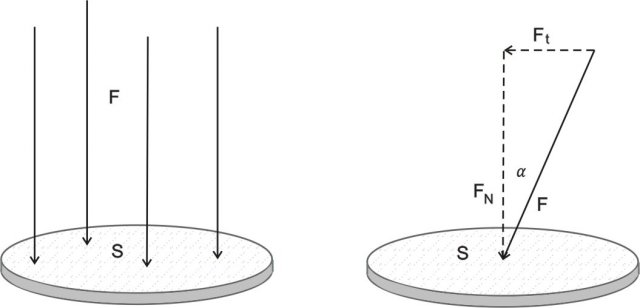
Slika 2: tlak sile. Leva slika: sila in ploskev sta pravokotni. Desna slika: sila deluje poševno na ploskev
Tlak sile p je sila deljeno s ploskvijo, na kateri deluje sila (slika 2 levo):
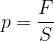
V kolikor sila ni pravokotna na ploskev (slika 2 desno), silo razdelimo na dve komponenti:
pravokotno ali normalno komponento 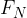 in na
in na
prečno ali tangencialno komponento 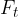
Tlak povzroča samo sila, ki je pravokotna na ploskev, tangencialna sila povzroča strižne napetosti, ki jih v tem poglavju ne bomo obravnavali.
Tlak sile izračunamo (upoštevamo le pravokotno komponento!):
Enota za tlak je paskal [Pa]:
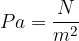
Večja enota je bar:
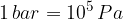
Tlak sile je:
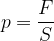
Če sila ni pravokotna na ploskev, vzamemo pravokotno komponenta sile:
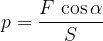
Enota za tlak je 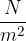 ali Pa (paskal). Večja enota je bar:
ali Pa (paskal). Večja enota je bar:
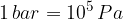
Obrnimo sedaj smer sile tako, da razteguje predmet (glej sliko 3). Na telo deluje natezna napetost, ki je enaka količniku med silo in ploskvijo.
Oznaka za natezno napetost je 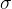 .
.
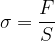
Enota za natezno napetost je enaka kot za tlak: paskal (Pa).
Natezno napetost računamo enako kot tlak, samo da uporabimo oznako 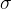 namesto p :
namesto p :
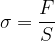
Tudi enota je enaka, kot za tlak, torej paskal [Pa].
Pod vplivom natezne napetosti se telo podaljša - glej sliko 4.
Opazujmo najprej, kako vpliva natezna napetost 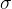 na podaljšek palice x. Prvotna dolžina palice naj bo l in definiramo lahko relativni raztezek palice
na podaljšek palice x. Prvotna dolžina palice naj bo l in definiramo lahko relativni raztezek palice  :
:
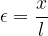
Relativni raztezek nima enote, saj se enoti v števcu in imenovalcu krajšata.
Pri razmeroma majhnih nateznih napetosti velja linearna odvisnost med natezno napetostjo in relativnim raztezkom:

Oznaka E pomeni modul elastičnosti. Odvisen je samo od izbrane snovi in ne od oblike telesa. Pove nam, kolikšna je potrebna natezna napetost za določen relativni raztezek:
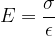
Enota za modul elastičnosti je 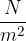 .
.
Slika 5 kaže odvisnost natezne napetosti od relativnega raztezka.
Graf na sliki 5 je razdeljen na štiri odseke:
Linearen odsek
V linearnem odseku velja enačba (1). Palica se linearno razteguje vse do točke, ki jo imenujemo mejo linearnosti. Če kadarkoli v tem območju zmanjšamo natezno napetost na 0, se bo palica vrnila v začetno, neraztegnjeno, stanje.
Nelinearni odsek
Ko palico raztegnemo čez mejo linearnosti - a ne presežemo meje elastičnosti enačba (1) ne velja več. Enačba (1) je samo linerani približev, v danem območju pa pridejo do izraza še nelinearni členi.
Enačba (1) sicer ne velja več, a če natezno napetost zmanjšamo na 0, se bo palica še vedno vrnila v začetno, neraztegnjeno, stanje.
Plastična deformacija
Če presežemo mejo elastičnosti a ne spresežemo meje trdnosti, se palica plastično (trajno) deformira. To pomeni, da tudi če zmanjšamo natezno napetost na 0, se palica ne vrne več v začetno neraztegnjeno stanje, temveč ostane trajno raztegnjena (glej črtkano črto na sliki 5).
Porušitev sistema
Če presežemo mejo trdnosti se palica poruši. To pomeni, da se palica še naprej razteza pri nespremenjeni natezni napetosti. Pri nadaljnem raztezanju se presek palice manjša in je zato pri isti sili potrebna manjša natezna napetost za večjo deformacijo palice. Palica se razteza, čeprav natezna napetost pada.
Prišli smo do meje trdnosti. Če v tej točki ne popusti natezna napetost, se palica zanesljivo poruši (zlomi, razbije, razcepi...). Za razlago pojava porušive palice glej tudi uvodno poglavje - slika 1.
Snov se pod vplivom natezne napetosti podaljša. V linearnem področju raztezanja velja enačba:
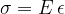
E je modul elastičnosti, ki je odvisen samo od snovi. Pri tem je  relativni podaljšek:
relativni podaljšek:
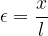
Tlak p deluje na palico tako, da jo krči - slika 6.
Zaradi tlaka se dolžina palice zmanjša za x. Tudi sedaj velja enačba (1), ki smo jo zapisali v prejšnjem poglavj, vsaj dokler smo v linearnem odseku, le da namesto natezne napetosti 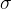 uporabimo oznako za tlak p:
uporabimo oznako za tlak p:
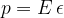
Pri čemer je  :
:
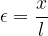
Kaj pa, če deluje tlak sile iz vseh smeri na telo. V tem primeru se telo stisne, zmanjša se mu volumen V za 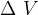 , kot kaže slika 7.
, kot kaže slika 7.
Relativno zmanjšanje volumna je sorazmerno spremembi tlaka na telo:

Preznak (-) pomeni, da se pri večjem tlaku volumen zmanjša.
Sorazmernostna konstanta 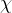 (izgovorjava hi) pomeni stisljivost snovi. Enota je
(izgovorjava hi) pomeni stisljivost snovi. Enota je 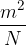 . Pri trdnih snoveh in tudi kapljevinah je stislljivost zelo majhna.
. Pri trdnih snoveh in tudi kapljevinah je stislljivost zelo majhna.
Relativna sprememba volumna je sorazmarna tlaku, ki deluje na vse telo.
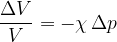
Faktor sorazmernosti 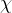 se imenuje stisljivost snovi in je odvisna samo od izbrane snovi, ne pa od geometrije snovi.
se imenuje stisljivost snovi in je odvisna samo od izbrane snovi, ne pa od geometrije snovi.