Osebne zbirke


Kompleksno število delimo s kompleksnim številom tako, da deljenje zapišemo v obliki ulomka in ulomek razširimo (množimo števec in imenovalec) s konjugiranim kompleksnim številom imenovalca, s čimer odpravimo imaginarno enoto iz imenovalca.
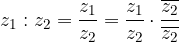
Poglejmo si deljenje kompleksnih števil na konkretnem primeru:
Velja:
Za vsako kompleksno število z, ki je različno od 0, obstaja obratno število, ki je 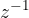 .
.
Obratno število izračunamo s pomočjo postopka za deljenje kompleksnih števil, se pravi tako, da ga zapišemo v obliki ulomka in ulomek razširimo (množimo števec in imenovalec) s konjugiranim kompleksnim številom, s čimer odpravimo imaginarno enoto iz imenovalca:
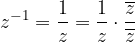
Poglejmo si postopek izračuna obratnega števila na konkretnem primeru: