Osebne zbirke


Ko neko telo premaknemo, opravimo delo. Če ga ne bi bomo mogli premakniti s silo lastnih rok, lahko uporabimo orodje. Orodje bomo uporabili tudi zato, da si olajšamo delo.
Že od nekdaj so si ljudje pomagali z orodji. Seveda si danes lahko pomagamo tudi z električnim orodjem. Včasih je uporaba električnega orodja nujna, vendar ne nadomešča vselej klasičnega orodja.
Osnovno delovanje orodja bomo spoznali na naslednjih primerih orodij:
klanec,
škripec,
vzvod.
Orodje je pripomoček, s pomočjo katerega opravimo delo, ki ga drugače ne bi zmogli. Lahko pa si z orodjem olajšamo delo. To pomeni, da opravimo enako delo z manjšo silo.
V gradivu delo smo se naučili, da je delo 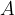 produkt sile in poti. Zapišimo to še z enačbo:
produkt sile in poti. Zapišimo to še z enačbo:
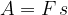
oziroma, če izrazimo silo:
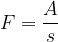
Iz enačbe vidimo, da sta pri istem delu sila in pot obratno sorazmerni. Oglejmo si to na dveh primerih.
Običajno nam delo otežuje prevelika sila, s katero bi morali delovati. Zato nam je lažje, če lahko uporabimo manjšo silo, čeprav z njo delujemo na daljši poti.
Orodja so pripomočki, s pomočjo katerih z manjšo silo opravimo enako delo, kot brez orodja. Pri vseh orodjih velja, da se na račun manjše sile podaljša pot, na kateri deluje sila. Velja:
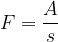
Pri določenem opravljenem delu A, je sila obratno sorazmerna s potjo.
V tem primeru dvigujemo tovor na določeno višino. Za navpični dvig je tovor pretežak. Pomagamo si lahko s klancem. Namesto, da bi dvigovali tovor navpično navzgor, si s pomočjo desk napravimo klanec.
Sila, ki je zdaj potrebna, je:
tolikokrat manjša,
kolikokrat je daljši klanec, v primerjavi z višino, na katero moramo dvigniti tovor.
Sila 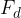 , s katero vlečemo ali potiskamo breme na klancu, je tolikokrat manjša od teže
, s katero vlečemo ali potiskamo breme na klancu, je tolikokrat manjša od teže 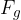 bremena, kolikokrat je dolžina klanca daljša od višine klanca:
bremena, kolikokrat je dolžina klanca daljša od višine klanca:
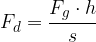
Pri tem je 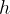 višina klanca in
višina klanca in  dolžina klanca.
dolžina klanca.
Vzvod je v osnovi dolga palica. Palico na določenem mestu podpremo. Točko podpore imenujemo vrtišče. Vrtišče mora biti bliže težjemu predmetu. Z nasprotnim, daljšim koncem palice (ročajem), lahko dvignemo težak predmet s silo, ki je manjša od teže predmeta.
Če je ročaj 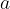 desetkrat daljši od krajšega delovnega konca
desetkrat daljši od krajšega delovnega konca 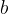 , potem bomo z roko dvignili kamen z desetkrat manjšo silo
, potem bomo z roko dvignili kamen z desetkrat manjšo silo 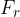 kot je teža kamna
kot je teža kamna 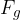 . Pri tem pa na z roko opravimo desetkrat daljšo pot od dviga kamna.
. Pri tem pa na z roko opravimo desetkrat daljšo pot od dviga kamna.
Pri vzvodu je sila roke 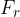 tolikokrat manjša od teže
tolikokrat manjša od teže 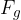 bremena, kolikokrat je ročaj vzvoda daljši od delovnega konca vzvoda:
bremena, kolikokrat je ročaj vzvoda daljši od delovnega konca vzvoda:
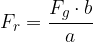
Pri tem je:
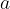 ročaj vzvoda - dolžina od prijemališča roke do vrtišča vzvoda,
ročaj vzvoda - dolžina od prijemališča roke do vrtišča vzvoda,
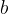 pa je delovni konec vzvoda - dolžina od vrtišča do bremena na vzvodu.
pa je delovni konec vzvoda - dolžina od vrtišča do bremena na vzvodu.
Poglejmo še nekaj primerov uporabe vzvoda.
Po načelu vzvoda delujejo še številna druga orodja. Primer so klešče, škarje, izvijač itd. Spoznali jih bomo v vajah.
Škripec je pogosto uporabljeno orodje za dvigovanje težjih predmetov. To je kolo, preko katerega je speljana vrv.
Ogledali si bomo dve možnosti izvedbe škripca, to sta:
pritrjeni škripec in
gibljivi škripec.
Če je telo škripca fiksno pritrjeno na nosilno ogrodje, govorimo o pritrjenemu škripcu. Običajno je škripec pritrjen na strop ali steno.
Na enem koncu vrvi je obešen tovor, na drugem koncu vlečemo vrv. S pritrjenim škripcem spreminjamo samo smer vlečne sile, ne pa njene velikosti.
Pritrjeni škripec uporabljamo zato, da lahko prilagajamo smer vlečne sile. Velikost vlečne sile 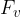 pa ni nič zmanjšana in je enaka teži
pa ni nič zmanjšana in je enaka teži 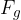 bremena:
bremena:
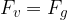
Gibljivi škripec omogoča, da breme dvignemo z manjšo silo od teže bremena. Pri gibljivemu škripcu en konec vrvi pritrdimo na nosilno ogrodje (strop, steno), kot kaže slika 5. Vrv nato speljemo preko gibljivega škripca in na škripec pritrdimo breme.
Škripec z bremenom torej visi na dveh vrveh, pri čemer vsaka vrv nosi polovico teže bremena - slika 5 desno. En konec vrvi je pritrjen na ogrodje, drugi konec vrvi vlečemo z roko. Sila vlečenja je polovica teže bremena.
Ko dvigujemo konec vrvi z roko, se hkrati dviguje tudi škripec z bremenom. Pri potegu vrvi je premik roke dvakrat daljši od dviga bremena. Zato je tudi sila dvakrat manjša.
Pri gibljivih škripcih se sila bremena razdeli na več vzporednih sil vrvi, ki nosijo tovor. Vlečna sila je manjša od teže tovora. Zmanjša se tolikokrat, kolikor je vzporednih vrvi, na katere je obešen tovor. Velja enačba:
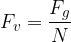
Tu je:
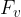 vlečna sila roke
vlečna sila roke
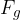 teža tovora
teža tovora
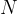 število vrvi, na katere je pritrjen tovor
število vrvi, na katere je pritrjen tovor
Teža tovora se razporedi med več vzporednih vrvi, kjer vsaka nosi enak delež teže bremena. Zato je vlečna sila manjša od teže tovora. Zmanjša se s številom vrvi - vzporednih sil, ki nosijo tovor. Velja enačba:
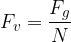
kjer je N število vzporednih vrvi, ki nosijo tovor. Pri enem gibljivem škripcu je število N vrvi enako 2. Pri dveh gibljivih škripcih je N enak 4 in tako naprej. Število vrvi je dvakrat večje od števila gibljivih škripcev.
Za enak faktor N, kot se zmanjša vlečna sila, se poveča pot vrvi, s katero dvigujemo tovor.
Če uporabimo več gibljivih škripcev, dobimo škripčevje. V tem primeru se teža bremena razdeli med več vrvi, ki povezujejo gibljive škripce.
Gibljive škripce lahko združujemo tudi enega za drugim. Pri tem še vedno velja, da vsak gibljivi škripec prispeva po dve vrvi.