Osebne zbirke


Ko dvigujemo uteži, opravljamo delo, prav tako ko zabijamo žeblje, dvigujemo kramp, kopljemo z lopato ali ko potiskamo avto - v vseh teh primerih opravljamo delo. Podobnih zgledov je še veliko, za vse je značilno, da s silo nekaj premikamo. Ugotovimo lahko tudi, da z večjo silo in dlje kot nekaj premaknemo, več dela opravimo. Od tod tudi pridemo do naslednje definicije dela:
Delo, ki ga označujemo s črko A, je definirano kot skalarni produkt vektorja stalne sile 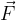 in vektorja premika prijemališča sile
in vektorja premika prijemališča sile 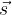 .
.
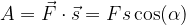
Kjer je 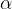 kot med stalno silo in smerjo premikanja.
kot med stalno silo in smerjo premikanja.
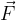 je vektor stalne sile, kar pomeni, da se velikost sile ne spreminja, ampak delujemo s konstantno silo.
je vektor stalne sile, kar pomeni, da se velikost sile ne spreminja, ampak delujemo s konstantno silo.
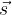 je vektor premika prijemališča sile, ki nam pove kam in za koliko se je prijemališče sile premaknilo.
je vektor premika prijemališča sile, ki nam pove kam in za koliko se je prijemališče sile premaknilo.
Enota za delo je J (Joule). Delo 1J opravi stalna sila 1N pri premiku telesa (prijemališča sile) za 1m:
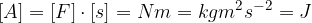
Imejmo za primer mamo, ki potiska nakupovalni voziček. Ko mama potiska nakupovalni voziček, opravlja delo. Če potiska s konstantno silo 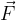 v smeri gibanja -
v smeri gibanja - 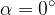 - in potisne voziček za
- in potisne voziček za  daleč, lahko delo izračunamo po enačbi:
daleč, lahko delo izračunamo po enačbi:
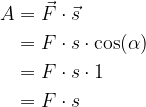
V primeru, da imamo v nakupovalnem vozičku tudi otroka, otrok tudi potiska voziček s svojo težo, vendar pravokotno v smeri gibanja - 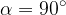 - in zato ne opravlja dela, saj če izračunamo delo po enačbi:
- in zato ne opravlja dela, saj če izračunamo delo po enačbi:
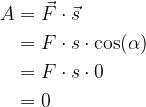
Kadar pa potiskamo s konstantno silo v smeri gibanja pod kotom 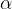 , uporabimo enačbo za izračun dela:
, uporabimo enačbo za izračun dela:
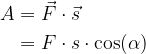
Oglejmo si primer vrtenja, ki ga prikazuje spodnja slika, ko na kolut navito cev vlečemo s stalno silo 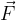 . Ko se kolut zavrti za kot
. Ko se kolut zavrti za kot 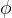 naredi cev pot
naredi cev pot 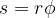 . Smer sile je v našem primeru tangentna, kar pomeni, da je kot med silo in smerjo vrtenja
. Smer sile je v našem primeru tangentna, kar pomeni, da je kot med silo in smerjo vrtenja 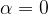 . Tako lahko delo izračunamo po enačbi:
. Tako lahko delo izračunamo po enačbi:
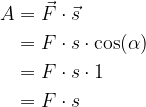
In če še upoštevamo, da je 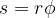 , Lahko zapišemo:
, Lahko zapišemo:
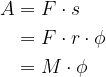
Na koncu smo delo še zapisali z navorom M, saj je navor produkt sile in ročice 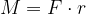 .
.
Delo sile pri vrtenju je torej enako produktu navora sile in zasuka:
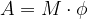
V primeru, da sila ni v tangentni smeri, se pravi kot med silo in smerjo vrtenja 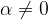 , upoštevamo samo tangentno komponento
, upoštevamo samo tangentno komponento 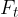 . Tako dobimo enačbi:
. Tako dobimo enačbi:
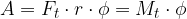
Za definiranje dela tlaka, si poglejmo spodnji bat, ki pritiska na tekočino v valju s stalno silo 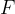 in se pri tem premakne za pot
in se pri tem premakne za pot  . Opravljeno delo je enako
. Opravljeno delo je enako 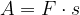 . Silo lahko zapišemo tudi s tlakom
. Silo lahko zapišemo tudi s tlakom 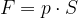 , kjer je
, kjer je 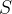 presek bata (površina osnovne ploskve) in dobimo:
presek bata (površina osnovne ploskve) in dobimo:
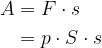
Produkt 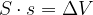 nam da volumen valja z osnovno ploskvijo
nam da volumen valja z osnovno ploskvijo 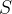 in višino
in višino  , ki je enak volumnu izrinjene tekočine. Tako lahko zapišemo:
, ki je enak volumnu izrinjene tekočine. Tako lahko zapišemo:
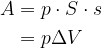
Delo tlaka je torej enako produktu tlaka, pod batom in prostornini izrinjene tekočine.
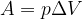
V veliki večini primerov, nas ne zanima kakšno delo je bat oddal tekočini, temveč kakšno delo je opravila zunanja sila s potiskanjem bata. Ko z zračno tlačilko napihujemo žogo, nas ne zanima delo, ki ga je opravil bat, temveč koliko dela smo mi vložili za potiskanje bata. Zato moramo še upoštevati, da na zunanji strani bata deluje sila zračnega tlaka, ki nam pomaga pri potiskanju:
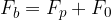
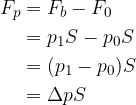
Delo sile s katero potiskamo bat tako lahko izračunamo z enačbo: