Prijava z e-naslovom
Prijava brez gesla
V limiti diferenčnega kvocienta je sprememba neodvisne spremeljivke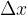 
neskončno majhna. Označimo jo z 
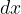. Tudi sprememba funkcijske vrednosti 
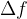je zaradi zveznosti funkcije f ustrezno majhna. Označimo jo z 
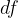. Tako dobimo odvod:
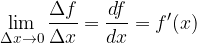
iz česar izpeljemo:
Diferencial funkcije df izpeljemo iz gornje enačbe oziroma iz odvoda:
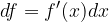
Diferencial funkcije f označimo z 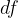in je enak
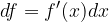
Diferencial funkcije nam pove, za koliko se spremeni ordinata pri spremembi abscise dx na tangenti v točki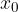 
(in ne na grafu funkcije!). Pri majhni spremembi x, je diferencial funkcije na tangenti skoraj enak spremembi ordinate funkcije in ga lahko vzamemo za dober približek spremembe funkcije.
Za lažje razumevanje pokažimo to grafično:
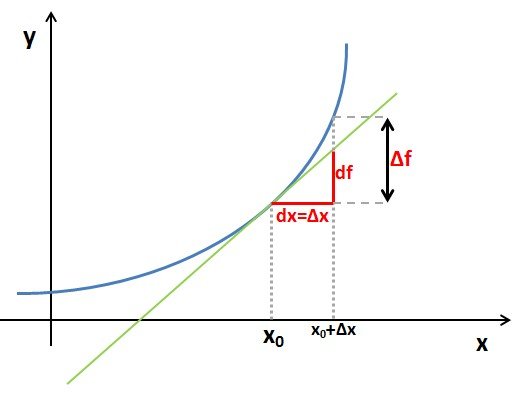
Diferencial df na tangenti, je pri majhni spremembni dx skoraj enak spremembi same funkcije 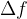zato lahko v približku zapišemo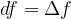 
Diferencial pogosto uporabljamo tudi pri približnem računanju funkcijskih vrednosti. Navadno to storimo takrat, ko je računanje prave funkcijske vrednosti prezapleteno.
Približno funkcijsko vrednost izračunamo s formulo:
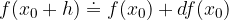
oziroma, če izpišemo diferencial:
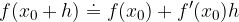
S pomočjo odvoda izpeljimo formulo za računanje približnih funkcijskih vrednosti:
Če torej iščemo vrednost funkcije f v točki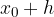 
, poznamo pa funkcijsko vrednost v točki 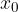, le-tej prištejemo diferencial funkcije in dobimo približno vrednost 
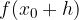. Namesto pravega prirastka funkcije smo prišteli diferencial, ki pa pomeni prirastek linearne funkcije - tangente na krivuljo. Poglejmo si grafično:
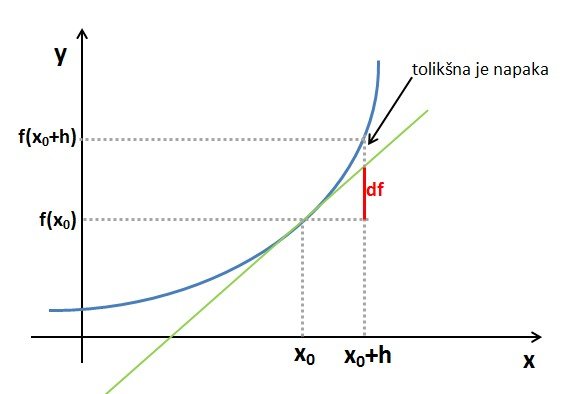
Na grafu je jasno naznačena napaka, ki jo storimo, ko uporabimo enačbo za izračun približne vrednosti funkcije.
