Prijava z e-naslovom
Prijava brez gesla
V klasični fiziki za maso velja ohranitveni zakon, ki pravi, da masa ne more izginiti ali nastati iz niča. Kot pa je ugotovil Einstein, to ne drži povsem, saj se lahko masa pretvori v energijo in obratno.
Delež mase, ki se pri vsakdanjih pojavih v telesih pretvori v energijo (ali obratno), je zelo majhen v primerjavi s celotno maso telesa, zato teh sprememb ne zaznamo niti z najbolj natančnimi merilnimi napravami. Drugače pa je pri reakcijah v jedru, kjer so te spremembe dovolj velike, da jih lahko izmerimo.
Povezavo med maso telesa in energijo, ki je v taki masi skrita, je prvi določil Einstein in jo opisuje enačba:
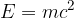
kjer je:
E energija, ki bi jo dobili, če bi se celotna masa m pretvorila v energijo,
m masa telesa,
c hitrost svetlobe, ki je konstanta in znaša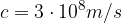 
.
Če telesu dodamo (ali odvzamemo) nekaj energije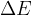 
- če ga npr. segrejemo, dvignemo ali če interagira z drugimi delci - se mu hkrati z energijo poveča (ali zmanjša) tudi masa in sicer za:
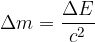
Pri reakcijah v jedru so:
mase, ki sodelujejo, dovolj majhne in
energije, ki se lahko sprostijo, dovolj velike,
da lahko spremembe mase že izmerimo.
Kot je opisano v gradivu Atomsko jedro, je masni defekt jeder razlika med:
masami prostih protonov in nevtronov ter
maso jedra v katerem so ti isti protoni in nevtroni združeni.
Ta razlika v masah je posledica energije, ki je sproščena pri nastanku jedra ali porabljena za njegovo razbitje.
Povezavo med spremembo mase in sproščeno ali porabljeno energijo opisuje Einsteinova energijska enačba:
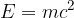
V prejšnjih poglavjih smo opisovali maso telesa, ko telesu dovajamo energijo v obliki toplote ali potencialne energije. Kaj pa se zgodi z maso telesa, če mu dovajamo kinetično energijo in ga torej pospešujemo?
V posebni teoriji relativnosti lahko napišemo polno energijo telesa z enačbo:
Energija gibajočega telesa se razdeli na:
kinetično energijo in
energijo telesa, ko je pri miru,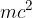 
.
Slednji člen, 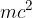, imenujemo mirovna energija, maso m mirujočega telesa pa mirovno maso. V prejšnjem razdelku smo videli, da se mirovna masa telesa spreminja, če mu dodajamo ali odvzemamo (toplotno ali potencialno) energijo z enačbo:
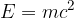
V določenih primerih, bi radi tudi v primeru kinetične energije uporabili slednjo enačbo. To lahko storimo, če uvedemo relativistično maso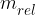 
in energijo napišemo kot:
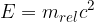
Poglejmo si jo podrobneje, kaj se skriva pod relativistično maso. V relativnostni teoriji kinetična energija ni več enaka:
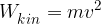
kot to velja v klasični fiziki, temveč se spremeni v:
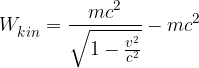
Polna energija je, kot smo omenili enaka:
Tako posplošena masa pa je odvisna od hitrosti. Z naraščanjem hitrosti narašča tudi relativistična masa telesa.
V posebni teoriji relativnosti se polna energija telesa lahko napiše kot:
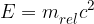
kjer je 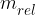relativistična masa. Relativistična masa je enaka:
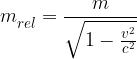
kjer je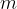 
masa telesa v mirovanju.
