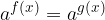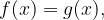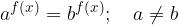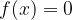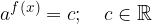Eksponentne enačbe so enačbe, v katerih neznanka nastopa v eksponentu.
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Z eksponentno enačbo se običajno srečamo, kadar želimo izračunati presečišče grafa eksponentne funkcije s katero koli drugo funkcijo, npr. linearno, kvadratno, eksponentno.
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Reševanje eksponentnih enačb
Eksponentne enačbe razlikujemo glede na postopek s katerim jih rešimo.
Eksponentne enačbe, ki jih prevedemo na enako osnovo
Nekatere eksponentne enačbe se dajo preoblikovati tako, da na obeh straneh enačaja nastopata le potenci z enakima osnovama:
Rešujemo jo tako, da enačimo eksponenta:
kar sledi iz injektivnosti eksponentne funkcije.
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Eksponentne enačbe z različno osnovo in enakimi eksponenti
Grafa eksponentnih funkcij z različnima osnovama se sekata na ordinatni osi, zato mora veljati:
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Enačbe, ki jih rešujemo z uvedbo nove neznanke
Nekatere enačbe lahko poenostavimo, če vpeljemo novo neznanko.
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Enačbe, ki jih rešujemo grafično
Enačbe, v katerih nastopajo eksponentne in ne-eksponentne funkcije, lahko rešimo le grafično. Pri teh enačbah najprej narišemo grafa obeh funkcij, ki ju vsebuje enačba. Z grafa približno preberemo rešitve enačbe, nato pa rešitev potrdimo z računom.
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Reševanje z izpostavljanjem skupnega faktorja
Eksponentne enačbe, kjer se pojavi vsota ali razlika potenc z enakimi osnovami, rešujemo z izpostavljanjem skupnega faktorja. Enačbo s tem prevedemo na že znane eksponentne enačbe.
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Reševanje z logaritmiranjem
Z logaritmiranjem se rešujejo enačbe tipa:
To so enačbe, ki imajo na obeh straneh različni osnovi in različna eksponenta. Reševanje teh enačb bomo spoznali pri logaritemskih enačbah.
Eksponentna neenačba
Eksponentne neenačbe so neenačbe, v katerih neznanka nastopa v eksponentu. Neenačbe običajno rešujemo grafično. To pomeni, da narišemo oba grafa, ki v neenačbi nastopata. Lahko pa jih rešimo tudi računsko.
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »