Osebne zbirke


Električni nihajni krog je električno vezje, ki služi za generacijo visokofrekvenčne izmenične napetosti. V osnovi je "električno" nihalo, sestavljeno iz vzporedne vezave kondenzatorja in tuljave.
Značilno za električni nihajni krog je, da se energija električnega polja kondenzatorja periodično pretaka v energijo magnetnega polja tuljave in obratno. Če postavimo analogijo z mehanskim nitnim nihalom, predstavlja nabit kondenzator potencialno energijo in tuljava kinetično energijo.
Predpostavimo, da je nihanje nihajnega kroga harmonično in da se napetost na kondenzatorju (in tuljavi, saj sta vezana vzporedno) spreminja po kosinusu:

Zaradi časovnega spreminjanja napetosti se spreminja tudi naboj na kondenzatorju:
Dobili smo funkcijo toka, katere maksimalna vrednost je:

Povzemimo. Ob predpostavki, da velja:
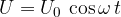
smo izpeljali
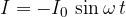
in velja
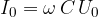
To poglavje je namenjeno učencem, ki so že osvojili poglavje odvodov. Učenci brez znanja odvodov lahko to poglavje brez škode preskočijo - pri tem pa še vedno lahko sledijo razlagi v nadaljevanju.
Želimo izpeljati:
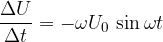
pri tem pa vemo, da:
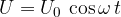
Znak 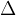 je velikokrat uporabljen kot srednješolski nadomestek odvoda
je velikokrat uporabljen kot srednješolski nadomestek odvoda 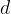 .
. 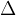 pomeni razliko (npr. časovno razliko), ta razlika pa je lahko poljubno velika. Znak
pomeni razliko (npr. časovno razliko), ta razlika pa je lahko poljubno velika. Znak 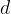 , tako kot
, tako kot 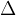 , prav tako pomeni razliko, a le neskončo majhno razliko.
, prav tako pomeni razliko, a le neskončo majhno razliko.
Enačba:
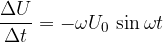
je pravzaprav samo srednješolski približek; prava enačba se glasi:
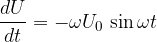
oziroma: iščemo odvod napetosti po času. Iz teorije odvodov pa vemo, da velja:
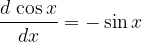
ter zato posledično:
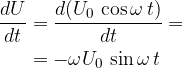
Zaradi spreminjajočega se toka (2) se v tuljavi inducira napetost:
Ponovno smo dobili kosinusno obliko napetosti, kakršna je tudi na kondenzatorju - enačba (1). To je razumljivo, saj je inducirana napetost na tuljavi vsak trenutek enaka napetosti na kondenzatorju (elementa sta vezana vzporedno).
To poglavje je namenjeno učencem, ki so že osvojili poglavje odvodov. Učenci brez znanja odvodov lahko to poglavje brez škode preskočijo - pri tem pa še vedno lahko sledijo razlagi v nadaljevanju.
Želimo izpeljati:
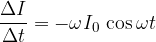
pri čemer smo enačbo (2) za tok izpeljali že v prejšnjem poglavju:
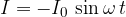
Znak 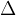 je velikokrat uporabljen kot srednješolski nadomestek odvoda
je velikokrat uporabljen kot srednješolski nadomestek odvoda 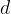 .
. 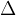 pomeni razliko (npr. časovno razliko), ta razlika pa je lahko poljubno velika. Znak
pomeni razliko (npr. časovno razliko), ta razlika pa je lahko poljubno velika. Znak 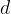 , tako kot
, tako kot 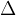 , prav tako pomeni razliko, a le neskončno majhno razliko.
, prav tako pomeni razliko, a le neskončno majhno razliko.
Enačba:
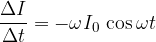
je pravzaprav samo srednješolski približek; prava enačba se glasi:
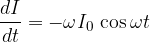
oziroma: iščemo odvod napetosti po času. Iz teorije odvodov pa vemo, da velja:
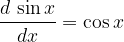
ter zato posledično:
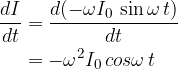
Če vzbudimo nihajni krog npr. tako, da s pomočjo zunanje napetosti nabijemo kondenzator, krog zaniha z lastno frekvenco.
Da bi izračunali lastno frekvenco nihanja, izenačimo napetost na kondenzatorju (1) in napetost na tuljavi (4):
Dobili smo izraz za frekvenco nihajnega kroga. Istočasno smo pokazali, da je nihanje res harmonično, saj v nasprotnem primeru ne bi mogli izenačiti napetosti na tuljavi in kondenzatorju.
Lastna ali resonančna frekvenca nihajnega kroga je:
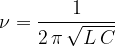
Med nihanjem nihajnega kroga se energija pretvarja iz električne energije kondenzatorja v energijo magnetnega polja tuljave tako, tako, da je vsota obeh energij v vsakem trenutku konstantna.
Predpostavimo, da je prvi trenutek vsa energija v kondenzatorju, saj je takrat na njemu maksimalna napetost (glej sliko Graf funkcije napetosti in toka nihajnega kroga)
Energija kondenzatorja je enaka delu, potrebnem da napolnimo kondenzator (glej tudi poglavje Kondenzator) do napetosti U. Je enaka ploščini pod grafom funkcije, ki kaže odvisnost naboja na kondenzatorju od napetosti.
Če pogledamo graf funkcije napetosti in toka vidimo, da je četrt periode od začetka opazovanja napetost na kondenzatorju nič. Kondenzator tedaj nima energije, vsa energija je v energiji magnetnega polja tuljave, skozi katero teče sedaj maksimalni tok:
Po Lenzovem pravilu se tuljava zaradi napetosti U lastne indukcije upira spremembam toka. Da steče skozi tuljavo naboj 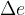 potrebujemo delo, ki je enako ploščini pod grafom napetosti U(e):
potrebujemo delo, ki je enako ploščini pod grafom napetosti U(e):
Vsak trenutek je vsota električne in magnetne energije konstanten in enak maksimalni energiji električnega ali magnetnega polja:
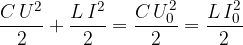
Še enkrat preverimo veljavnost enačbo za lastno frekvenco. V ta namen izenačimo maksimalni vrednostjo električne in magnetne energije:
Preko energije smo prišli do istega izraza za lastno frekvenco nihajnega kroga kot pri prvotnem izračunu.
Ponovimo:
Električna energija kondenzatorja:
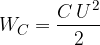
se v električnem nihajnem krogu harmonično preliva v magnetno energijo tuljave:
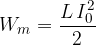
Vsota obeh energij je vsak trenutek konstantna in enaka maksimalni energiji tuljave ali kondenzatorja.
Energija niha z dvojno frekvenco napetosti.