Osebne zbirke


Elipsa je množica vseh točk 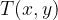 v ravnini, za katere je vsota razdalj od dveh fiksnih točk
v ravnini, za katere je vsota razdalj od dveh fiksnih točk 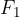 ,
, 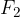 konstanta.
konstanta.
Geometrijsko definicijo elipse lahko zato zapišemo kot:
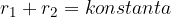
geometrijsko definicijo pa lahko lepo vidimo na sliki:
Matematično je, za enačbo elipse kot krivulje drugega reda, značilno, da imata kvadratna člena enak predznak in 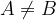 :
:
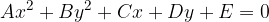
Značilne elemente elipse najlažje preberemo s pomočjo skice:

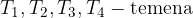
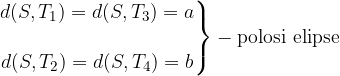
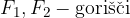

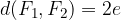
Elipsa ima dve polosi:
veliko polos: je razdalja od središča do bolj oddaljenega temena; običajno jo označimo z a. Gorišči elipse ležita vedno na veliki polosi.
malo polos: je razdalja od središča do manj oddaljenega temena; običajno jo označimo z b.
Pomebna lastnost elipse je še numerična ekscentričnost, ki je določena z:
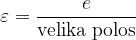
Numerična ekscentričnost elipse nam pove, kako sploščena je elipsa. Numerična ekscentričnost leži vedno na intervalu 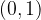 .
.
To poglavje ni bistvenega pomena za razumevanje snovi, zato ga lahko bralec tudi izpusti. Namenjeno je tistim učencem, ki si želijo snov poglobiti.
Pri izpeljevanju enačbe si bomo pomagali s sliko:
Začnimo z geometrijsko definicijo elipse:
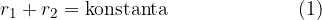
Prvi korak, ki ga moramo narediti, je, da določimo vrednost konstante. Konstanto določimo tako, da se postavimo v točko B in iz slike preberemo (glej predhodnje poglavje: Značilni elementi elipse):
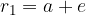
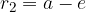
V enačbo 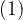 vstavimo
vstavimo 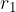 in
in 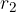 in dobimo:
in dobimo:
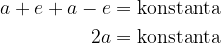
Dobljeno konstanto vstavimo nazaj v prvotno enačbo in zapišemo:
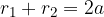
Naslednji korak izpeljave je, da izrazimo 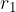 in
in 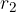 s pomočjo koordinate x in y. To naredimo s pravokotnimi trikotniki: trikotnika
s pomočjo koordinate x in y. To naredimo s pravokotnimi trikotniki: trikotnika 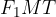 in
in 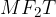 sta pravokotna, zato lahko zapišemo zanju pitagorov izrek:
sta pravokotna, zato lahko zapišemo zanju pitagorov izrek:
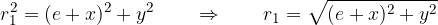
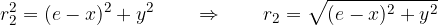
Končno lahko izpeljemo enačbo elipse:
Tako dobimo iskano enačbo elipse v središčni legi:
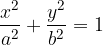
Enačba elipse s središčem v koordinatnem izhodišču v segmentni (odsekovni) obliki:
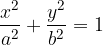
Opazimo lahko, da če velja a = b, se elipsa pretvori v krožnico.
Elipsa je lahko orientirana na dva različna načina in sicer:
a > b, oziroma a predstavlja veliko polos, b pa malo;
b > a, oziroma b predstavlja veliko polos, a pa malo.
Oglejmo si obe orientaciji.
Značilne elemente elipse najlažje preberemo s pomočjo skice:
Iz skice vidimo, da ima elipsa temena v točkah:
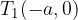
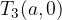
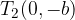
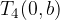
Gorišči elipse sta določeni z linearno ekscentričnostjo e:

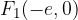
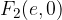
Numerična ekscentričnost elipse je:
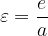
Če je b > a potem je elipsa raztegnjena v smeri ordinatne osi:
Iz skice vidimo, da ima elipsa temena v točkah:
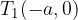
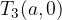
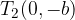
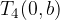
Gorišči elipse sta na ordinatni osi:
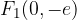
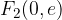
Linearno ekscentričnost elipse izračunamo:
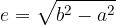
Numerična ekscentričnost elipse je:
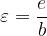
Če elipso vzporedno premaknemo tako, da pride središče v točko 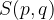 , ima premaknjena elipsa enačbo:
, ima premaknjena elipsa enačbo:
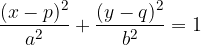
Oglejmo si na skici kako izgleda premaknjena elipsa:
Elipsa v premaknjeni legi ima središče v točki 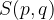
Značilne točke elipse v premaknjeni legi razberemo iz skice. Vidimo, da ima elipsa temena v točkah:
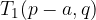
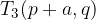
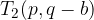
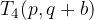
Gorišči elipse sta določeni z linearno ekscentričnostjo e:

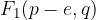
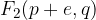
Numerična ekscentričnost elipse je: