Osebne zbirke


Telesa v naravi lahko mirujejo, se gibljejo enakomerno ali neenakomerno. Avto npr. pospešuje, vozi enakomerno ali zmanjšuje hitrost. Svojo vožnjo prilagaja razmeram na cesti. Isto velja za večino gibajočih se teles.
Opazujmo gibanje tekača na maratonu. Maratonec začne tek z zmernim tempom. Hitrost ni prevelika, saj hrani moč za drugo polovico proge. Njegovo gibanje je v začetku dokaj enakomerno. Šele v drugi polovici proge postopoma pospeši. Sedaj lahko prehiteva ostale tekače, ki so ga v začetku pustili za sabo. Sledi finiš. Takrat teče na vso moč, da bi dosegel čim boljši rezultat.
Tekač na dolgi progi se torej giblje neenakomerno. Njegova hitrost se spreminja s časom. Le v določenih krajših časih opazovanja lahko smatramo, da se giblje vsaj približno enakomerno.
V tem poglavju bomo obravnavali neenakomerno gibanje. Osredotočili se bomo na tisto neenakomerno gibanje, ko hitrost enakomerno narašča ali pada s časom. Pravimo mu enakomerno pospešeno ali enakomerno pojemajoče gibanje.
Telo se lahko giblje enakomerno ali neenakomerno.
Pri enakomernem gibanju se hitrost ne spreminja s časom. Pot izračunamo kot produkt hitrosti in časa. Zapišimo to z enačbo:
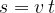
Kaj pa, če se hitrost spreminja s časom? Takšnemu gibanju pravimo neenakomerno gibanje. Med neenakomernim gibanjem se lahko hitrost s časom veča ali manjša. Govorimo o pospešenem gibanju ali pojemajočem gibanju.
Pri neenakomernem gibanju se hitrost s časom spreminja. Če se hitrost s časom veča, je to pospešeno gibanje. Če se hitros manjša pa je gibanje pojemajoče.
Posebni primer neenakomernega gibanja je enakomerno pospešeno gibanje. V tem primeru hitrost enakomerno narašča s časom. To pomeni, da se telesu v enakih časovnih presledkih hitrost poveča za enako vrednost.
Pri enakomerno pospešenem gibanju se nam hitrost enakomero spreminja. V vsakem opazovanem trenutku je hitrost drugačna. Pravimo ji trenutna hitrost.
Pri enakomerno pospešenem gibanju hitrost enakomerno narašča s časom. To pomeni, da je prirastek hitrosti v enako dolgih časovnih intervalih enak. Graf hitrosti v odvisnosti od časa je naraščajoča premica.
Trenutna vrednost hitrosti je hitrost v nekem opazovanem času t.
Uvedimo novo fizikalno količino: pospešek. Pospešek pove, kolikšen je prirastek hitrosti v opazovanem času. Oznaka za pospešek je a:
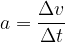
Znak 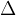 (grška črka Delta) pomeni razliko med končno in začetno vrednostjo:
(grška črka Delta) pomeni razliko med končno in začetno vrednostjo:
Sprememba hitrosti
Izračunamo jo kot: "hitrost na koncu opazovanega časovnega intervala" minus "hitrost na začetku intervala"
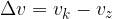
Sprememba hitrosti obdrži isto enoto kot hitrost: 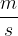 .
.
Časovna sprememba
Izračunamo jo kot: "čas na koncu opazovanega intervala" minus "čas na začetku intervala"
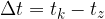
Časovna sprememba obdrži isto enoto kot čas:  .
.
Zapišimo splošno enačbo, po kateri izračunamo pospešek pri enakomerno pospešenem ali pojemajočem gibanju. Vanjo vstavimo tudi spremembi hitrosti in časa:
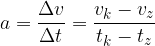
Sestavimo še enoto za pospešek. Ker nam pospešek pove, za koliko metrov na sekundo se poveča hitrost vsako sekundo, to zapišemo z enoto:
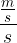
Ko poenostavimo dvojni ulomek, pa enoto zapišemo v obliki:
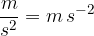
Če je začetna hitrost 0 m/s in čas začetka opazovanja 0 s, lahko napišemo pospešek v poenostavljeni obliki:
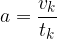
Pri enakomerno pospešenem gibanju hitrost narašča s časom, zato je končna hitrost večja od začetne hitrosti. To pa pomeni, da je sprememba (razlika) hitrosti pozitivna. Sledi, da je tudi pospešek je pozitiven.
Če je v opazovanem gibanju končni čas kar enak celotnemu času t in končno hitrost označimo z v, potem lahko v zgornji enačbi izpustimo indeks k:
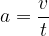
Obrnimo še enačbo in izrazimo trenutno hitrost v pri poljubnem času t:
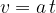
Pospešek pove, kolikšen je prirastek hitrosti v opazovanem času:
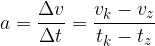
Pri enakomerno pospešenem gibanju je pospešek pozitiven in neodvisen od časa (konstanten).
Trenutno vrednost hitrosti v poljubnem času t pa izračunamo:
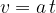
V poglavju Enakomerno gibanje za osnovno šolo smo si podrobneje pogledali, kako izračunati pot pri enakomernem gibanju, ko je hitrost stalna.
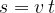
Pri enakomerno pospešenem gibanju hitrost ni stalna, zato bi bil izračun poti po zgornji enačbi napačen. Kako rešiti problem?
Najprej predpostavimo, da telo v začetku opazovanja miruje, nato pa določen čas enakomerno pospešuje.
Ker se hitrost enakomerno spreminja s časom, lahko večamo časovni interval opazovanja, ne da bi naredili napako. Namesto, da iščemo povprečno hitrost po posameznih intervalih, lahko izračunamo povprečno hitrost za celotni opazovani interval gibanja. Imenujemo jo povprečna hitrost celotnega in ji damo oznako 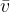 .
.
Povprečno hitrost enakomerno pospešenega gibanja izračunamo kot aritmetično sredino med začetno in končno hitrostjo:
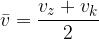
ali, če je začetna hitrost 0, potem je povprečna hitrost enaka:
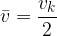
Povprečna hitrost gibanja je hitrost, s katero bi se moral predmet enakomerno gibati, da bi v enakem času opravil enako pot, kot pri neenakomernem gibanju.
Ko je začetna hitrost enaka nič, jo izračunamo po formuli:
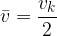
Formula za povprečno hitrost upošteva, da se telesu hitrost spreminja. Zato lahko s povprečno hitrostjo izračunamo opravljeno pot na podoben način, kot pri enakomernem gibanju:
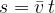
Poglejmo zgornjo sliko. Osredotočimo se na rdeče šrafiran pravokotnik in zeleno šrafiran trikotnik. Ploščini obeh likov sta enaki. Videli pa bomo, da ploščini obeh likov pomenita pot, ki jo opravi telo pri neenakomernem gibanju.
Rdeče šrafiran pravokotnik
Na ordinatni osi je točka, ki predstavlja povprečno hitrost 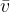 . Iz koordinatnega izhodišča narišimo pravokotnik s stranicami dolžine
. Iz koordinatnega izhodišča narišimo pravokotnik s stranicami dolžine 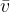 in
in 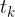 in mu izračunajmo ploščino.
in mu izračunajmo ploščino.
Ploščina pravokotnika je enaka produktu dolžine in širine. Torej 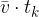 . Po zgornji formuli vidimo, da smo s tem izračunali pot s:
. Po zgornji formuli vidimo, da smo s tem izračunali pot s:
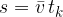
Zeleno šrafiran trikotnik
Popolnoma enako ploščino ima tudi trikotnik pod grafom hitrosti. Izračunamo jo po enačbi za izračun plošine trikotnika, torej:
Če pri opazovanem gibanju upoštevamo, da je čas na koncu opazovanega intervala kar celoten čas opazovanja, lahko v enačbi izpustimo indeks k:
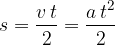
S pomočjo zgornje formule lahko narišemo še graf poti v odvisnosti od časa. Na časovni osi (abcisna os) označimo čase. Za vsak izbran čas po zgornji enačbi izračunamo razdaljo s in jo vnesemo na ordinatno os. Označimo točke, kjer se sekajo abcise in ordinate in jih povežemo s krivuljo.
Videli smo, da lahko pot pri enakomerno pospešenem gibanaju izračunamo na dva različna načina, ko je začetna hitrost enaka nič. Izračunamo jo lahko s časom t in:
povprečno hitrostjo
pospeškom
Pri enakomerno pospešenem gibanju (velja tudi za poljubno neenakomerno gibanje) izračunamo pot kot ploščino pod grafom hitrosti.
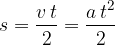
Izračunajmo jo lahko tudi kot produkt povprečne hitrosti in časa opazovanja:
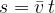
Grafi za enakomerno pospešeno gibanje z začetno hitrostjo 0
A: graf hitrosti v odvisnosti od časa
Hitrost enakomerno narašča s časom. To pomeni, da se hitrost v vsaki sekundi enako poveča. Graf je naraščajoča premica. Pot telesa lahko izračunamo kot ploščino pod grafom hitrosti.
B: Graf pospeška v odvisnosti od časa
Pospešek se ne spreminja. Graf je premica, brez naklona.
C: Graf poti v odvisnosti od časa
Telo v vsaki sekundi opravi daljšo pot, saj se se giblje vedno hitreje. Pot se s časom spreminja po krivulji, ki ji pravimo parabola.
Kaj pa, če začetna hitrost ni enaka nič? Pot računamo na podoben način kot v primeru, da je začetna hitrost nič. Tudi v tem primeru je pot enaka ploščini pod grafom hitrosti. Izračunamo jo lahko na dva načina:
Računanje poti s pomočjo povprečne hitrosti
Gibanje se začne z začetno hitrostjo 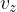 , nato pa hitrost enakomerno narašča do končne hitrosti
, nato pa hitrost enakomerno narašča do končne hitrosti 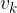 .
.
Povprečna hitrost je:
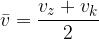
Celotna pot pa je enaka, kot če se bi gibal enakomerno s povprečno hitrostjo:
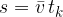
V zgornji enačbi lahko pri času t spustimo indeks k, če upoštevamo, da je čas t celotni čas opazovanja. Potem dobimo:
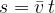
Računanje poti s pomočjo izračuna ploščine lika pod grafom hitrosti
Pot je enaka ploščini pod grafom hitrosti. Iz slike vidimo, da je lik pod grafom hitrosti sestavljen iz dveh likov:
pravokotnika
in trikotnika.
Ploščina pravokotnika pomeni pot, ki bi jo naredilo telo, če bi se enakomerno gibalo z začetno hitrostjo 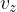 :
:
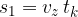
Pot, ki bi jo naredilo telo med pospeševanjem od začetne do končne hitrosti pa izračunamo s pomočjo ploščine trikotnika:
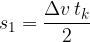
kjer je:
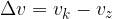
Pot bo enaka vsoti ploščin obeh likov:
Upoštevajmo še, da končni čas 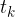 označuje celotni čas opazovanja, zato lahko izpustimo indeks k. Potem enačba dobi lepšo obliko:
označuje celotni čas opazovanja, zato lahko izpustimo indeks k. Potem enačba dobi lepšo obliko:
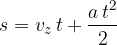
V primeru, da pri enakomerno pospešenem gibanju začetna hitrost ni enaka nič, računamo pot s pomočjo povprečne hitrosti:
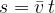
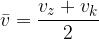
ali po enačbi:
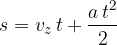
Telesu lahko hitrost s časom tudi enakomerno pada. Takemu gibanju pravimo enakomerno pojemajoče gibanje.
Izračunajmo pospešek za takšno gibanje.
Pospešek ima negativni predznak. Pravimo mu tudi pojemek.
Pot pa je:
Pri enakomerno pojemajočem gibanju hitrost enakomerno pada s časom. Graf hitrosti v odvisnosti od časa je padajoča premica.
Pospešek je negativen in konstanten. Je količnik začetne hitrosti in časa zaustavljanja.
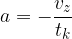
Pot je izračunamo kot:
Grafa za enakomerno pojemajoče gibanje.
A: Graf hitrosti v odvisnosti od časa
Hitrost enakomerno pada s časom. Graf je premica s padajočim (negativnim) naklonom.
Strmina premice predstavlja pojemek. Imenujemo ga tudi negativni pospešek.
Ploščina pod grafom hitrosti je pot.
B: Graf pospeška v odvisnosti od časa
Pospešek je negativen in se ne spreminja s časom. Graf je premica brez naklona (vzporedna s časovno osjo).
V naravi je gibanje skoraj vedno sestavljeno. Voznik avtomobila:
spelje s pospeševanjem,
nekaj časa vozi enakomerno,
na koncu se ustavi z zaviranjem.
Takšno gibanje lahko razdelimo na ločene intervale. Čas trajanja posameznega intervala označimo z 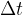 , kot kaže slika v spodnjem primeru.
, kot kaže slika v spodnjem primeru.
Povprečna hitrost pri gibanju je hitrost, ki jo bi imelo telo:
če bi se celotni čas 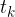 gibalo enakomerno,
gibalo enakomerno,
pri tem pa opravilo isto pot  , kot pri sestavljenem gibanju.
, kot pri sestavljenem gibanju.
Povprečno hitrost pri sestavljenem gibanju izračunamo tako, da delimo celotno pot s celotnim časom:
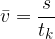
Pri sestavljenem gibanju razdelimo gibanje na intervale, kjer je gibanje pospešeno, pojemajoče ali enakomerno. Pot v posameznih intervalih je enaka ploščini lika pod grafom hitrosti. Celotna pot je:
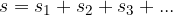
Povprečna hitrost je celotna pot deljena s celotnim časom: