Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Funkcijo si lahko predstavljamo kot škatlo, v katero vstavimo neko vrednost (vhodna vrednost), iz nje pa po določenem pravilu dobimo novo vrednost (izhodna vrednost). Nova vrednost se običajno razlikuje od prvotne, lahko pa je tudi enaka prvotni vrednosti.
Imenujmo množico vhodnih vrednosti množica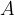 
, množico izhodnih vrednosti pa množica 
.
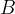V matematičnem jeziku je funkcija preslikava iz množice 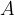v množico .
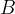Ti množici prestavljata dve medsebojno odvisni količini:
Prvo količino lahko poljubno izbiramo in spreminjamo. Imenujemo jo neodvisna spremenljivka in jo običajno označujemo z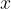 
.
Tudi druga količina se spreminja, a v odvisnosti od prve količine. Zato jo imenujemo odvisna spremenljivka in jo običajno označujemo z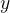 
.
Vrednost 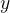, ki jo funkcija priredi določeni neodvisni spremenljivki 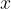, imenujemo funkcijska vrednost in jo označujemo tudi z 
.
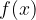Zapis 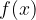označuje isto kot 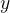. Le da zapis 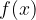poudarja, da je to neka izračunana vrednost, ki jo dobimo, ko s funkcijo 
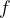preslikamo število .
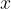Funkcija je predpis, ki vsakemu elementu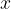 
iz množice 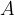priredi natanko en element 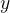v množici .
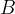Predpis funkcije je pravilo, ki vsaki vrednosti 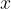priredi točno eno vrednost 
. Za predpis moramo tudi napisati, kakšen. To običajno zapišemo z enačbo ali pa s puščico, tako da je razvidno, v kaj se preslika poljuben element .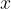
Predpis funkcije je pravilo, ki vsaki vrednosti 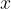iz množice 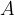priredi točno eno vrednost 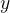iz množice .
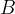Funkcijo lahko predstavimo na več načinov:
z enačbo,
s tabelo,
s puščičnim diagramom in
s prikazom vrednosti funkcije v koordinatnem sistemu.
Funkcijo lahko zapišemo v obliki enačbe, s katero lahko izračunamo vrednost funkcije 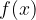za poljubno število .
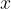Če vrednost funkcije izračunamo za več vrednosti 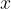, jih lahko uredimo v obliki tabele.
V prvi vrstici tabele navedemo vrednosti 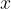, v drugi pa vrednosti 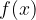oziroma .
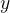Tabelo uredimo tako, da sta vrednost 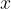in njej pripadajoča vrednost 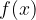ena pod drugo.
Funkcijo lahko predstavimo tudi s puščičnim diagramom. Na levo stran narišemo množico neodvisnih spremenljivk 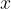, na desno pa množico vrednosti 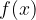. Na koncu povežemo vrednosti 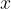in pripadajoče vrednosti 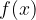s puščicami.
Spremenljivke 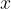in iz njih izračunane vrednosti 
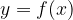lahko zapišemo kot urejene pare 
.
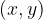Vsak tako napisan urejeni par lahko razumemo kot eno točko v koordinatnem sistemu:
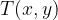
Ko narišemo vse urejene pare dane funkcije v koordinatni sistem, dobimo graf funkcije. Graf funkcije je torej množica vseh točk, ki jih dobimo s preslikavami dane funkcije.
Sedaj, ko poznamo že vse potrebno, razložimo še pojem vrednost funkcije.
Vrednost funkcije pri dani vrednosti 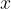je število, v katerega funkcija preslika dano vrednost.
Zapišemo jo kot .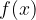
