Osebne zbirke


Če sta dve količini med seboj odvisni, zanju lahko zapišemo predpis, ki ga matematično imenujemo funkcija. Funkcijo lahko predstavimo na različne načine.
Dve količini sta lahko odvisni med seboj; pri tem eno imenujemo odvisna, drugo pa neodvisna spremenljivka:
odvisna spremenljivka: količina, ki je odvisna od druge količine; v matematiki jo označimo z 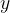 .
.
neodvisna spremenljivka: količina, ki se lahko poljubno (neodvisno) spreminja; v matematiki jo označimo z  .
.
Pravimo tudi, da je odvisna spremenljivka 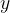 funkcija neodvisne spremenljivke
funkcija neodvisne spremenljivke  , in to zapišemo z:
, in to zapišemo z:
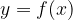
kjer je 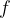 predpis,
predpis, 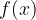 pa vrednost te funkcije pri danem
pa vrednost te funkcije pri danem  .
.
Funkcija je predpis, ki vsakemu elementu  iz množice
iz množice 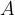 , priredi natanko en element iz množice
, priredi natanko en element iz množice 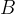 . Grafično to lahko ponazorimo s puščičnim diagramom.
. Grafično to lahko ponazorimo s puščičnim diagramom.
O funkciji ne moremo govoriti, kadar:
predpis ne preslika vseh elementov iz množice 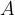
kakšen element iz množice 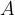 se preslika v dva ali več elementov v množici
se preslika v dva ali več elementov v množici 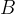
Dogovorili se bomo za naslednje označevanje:
funkcije poimenujemo s črkami:
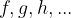
zapis 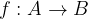 preberemo:
preberemo:
Funkcija 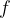 preslikuje iz množice
preslikuje iz množice 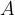 v množico
v množico 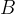 .
.
zapis 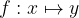 preberemo:
preberemo:
Funkcija 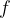 elementu
elementu  iz množice
iz množice 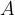 priredi element
priredi element 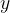 iz množice
iz množice 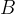 .
.
Definicijsko območje 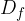 je množica, na kateri je definirana funkcija. Elemente imenujemo tudi imenujemo original.
je množica, na kateri je definirana funkcija. Elemente imenujemo tudi imenujemo original.
Zaloga vrednosti 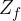 je množica vseh funkcijskih vrednosti
je množica vseh funkcijskih vrednosti 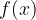 . Množica
. Množica 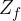 je lahko enaka množici
je lahko enaka množici 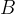 , v katero predpis slika ali pa je le njena podmnožica.
, v katero predpis slika ali pa je le njena podmnožica.
Funkcijo lahko predstavimo na različne načine. Najbolj pogosto jo predstavimo s predpisom. V primeru da sta definicijsko območje in zaloga vrednosti končni množici, lahko funkcijo predstavimo s tabelo ali s puščičnim diagramom. Realne funkcije pa lahko predstavimo tudi z grafom.
Funkcijo lahko podamo tako, da povemo kako funkcija originale spreminja v slike. To navedemo s predpisom:
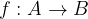
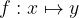
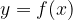
Funkcijo lahko podamo s tabelo v primeru, ko sta definicijsko območje in zaloga vrednosti končni množici. V prvo vrstico vnašamo vrednosti neodvisne spremenljivke, v drugo pa vrednosti odvisne spremenljivke.
Če pa govorimo o realni funkciji realne spremenljivke, preslikave ne moremo v celoti podati s tabelo. S tabelo si lahko ponazorimo le nekatere vrednosti funkcijskega predpisa.
Najprej narišemo dva diagrama, s katerima ponazorimo množico 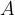 in množico
in množico 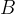 . S puščicami ponazorimo, kateri elementi množice
. S puščicami ponazorimo, kateri elementi množice 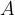 se preslikajo v elemente množice
se preslikajo v elemente množice 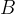 .
.
Graf funkcije je v matematiki osnovni način za prikaz funkcije. Graf funkcije 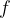 je definiran kot množica urejenih parov
je definiran kot množica urejenih parov 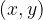 , kjer prvi element
, kjer prvi element  preteče celotno definicijsko območje funkcije, drugi element
preteče celotno definicijsko območje funkcije, drugi element 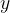 pa je slika pripadajočega
pa je slika pripadajočega  . Torej velja med komponentama zveza
. Torej velja med komponentama zveza 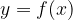 . Matematično to zapišemo kot:
. Matematično to zapišemo kot:
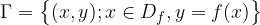
Kar preberemo: gama je množica vseh parov 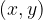 , kjer je
, kjer je  element množice definicijskega območja
element množice definicijskega območja 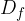 ,
, 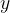 pa preslikava elementa
pa preslikava elementa  , v skladu s predpisom
, v skladu s predpisom 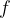 .
.
Urejene pare 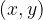 lahko narišemo v koordinatnem sistemu. Ko je množica
lahko narišemo v koordinatnem sistemu. Ko je množica 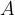 končna (ima končno število elementov), tedaj vsakemu elementu
končna (ima končno število elementov), tedaj vsakemu elementu 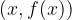 pripada v koordinatnem sistemu točka, katere abscisa je
pripada v koordinatnem sistemu točka, katere abscisa je  , ordinata
, ordinata 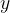 pa je njegova slika
pa je njegova slika 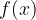 .
.
Če absciso točke 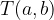 vstavimo v funkcijski predpis
vstavimo v funkcijski predpis 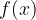 in kot rezultat dobimo ordinato te točke, potem točka
in kot rezultat dobimo ordinato te točke, potem točka 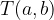 leži na grafu funkcije
leži na grafu funkcije 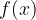 .
.
Če za točko 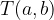 in funkcijo
in funkcijo 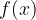 velja
velja
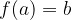 ,
,
potem točka 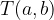 leži na grafu funkcije
leži na grafu funkcije 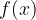 .
.
V naslednjih poglavjih se bomo naučili poiskati ničlo funkcije in njeno začetno vrednost.
Ničla funkcije je tisto število 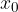 , pri katerem je vrednost funkcije
, pri katerem je vrednost funkcije 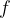 enaka 0. V koordinatnem sistemu ničlo funkcije vidimo v tisti točki, kjer graf funkcije seka ali se dotakne osi
enaka 0. V koordinatnem sistemu ničlo funkcije vidimo v tisti točki, kjer graf funkcije seka ali se dotakne osi  .
.
Če računsko iščemo ničlo 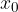 funkcije
funkcije 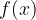 , potem vrednost poiščemo z nastavkom:
, potem vrednost poiščemo z nastavkom:
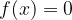
V linearni enačbi nastopa  na prvo potenco. Zaradi tega premici rečemo tudi, da je enačba prve stopnje; njeno ničlo imenujemo tudi enostavna ničla. Graf linearne funkcije seka abscisno os pod določenim neničelnim kotom.
na prvo potenco. Zaradi tega premici rečemo tudi, da je enačba prve stopnje; njeno ničlo imenujemo tudi enostavna ničla. Graf linearne funkcije seka abscisno os pod določenim neničelnim kotom.
Začetna vrednost je točka, kjer graf seka ordinatno 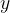 os. Ker točka leži na ordinatni osi je njena abscisa enaka 0, ordinato pa izračunamo tako, da za vrednost
os. Ker točka leži na ordinatni osi je njena abscisa enaka 0, ordinato pa izračunamo tako, da za vrednost  vstavimo 0:
vstavimo 0:
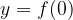
Točka je zato oblike: 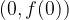 .
.
Vrednost funkcije je na določenem intervalu neodvisne spremenljivke lahko pozitivna, negativna ali pa je njena vrednost enaka 0.
Interval neodvisne spremenljivke obsega tista števila  , pri katerih je vrednost funkcije
, pri katerih je vrednost funkcije 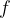 pozitivna, negativna ali enaka 0.
pozitivna, negativna ali enaka 0.
Za graf funkcije velja:
Na intervalu, kjer je vrednost funkcije večja od 0, se graf funkcije nahaja nad abscisno osjo.
Na intervalu, kjer je vrednost funkcije manjša od 0, se graf funkcije nahaja pod abscisno osjo.
V točkah, kjer je vrednost funkcije enaka 0, graf funkcije seka abscisno os.
Če ugotavljamo predznak funkcije računsko, vstavimo vrednost neodvisne spremenljivke v funkcijski zapis in pogledamo predznak rezultata.
Vrednost funkcije na določenem intervalu neodvisne spremenljivke lahko narašča, pada ali pa je njena vrednost konstanta.
Če se po  osi pomikamo v smeri večjih vrednosti in opazimo, da se povečuje tudi vrednost
osi pomikamo v smeri večjih vrednosti in opazimo, da se povečuje tudi vrednost 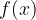 funkcije, potem funkcija narašča:
funkcije, potem funkcija narašča:
Če v določenem intervalu za vsak par neodvisnih spremenljivk 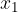 in
in 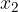 velja
velja
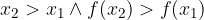
je v tem intervalu funkcija 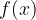 naraščajoča.
naraščajoča.
Če se po  osi pomikamo v smeri večjih vrednosti in opazimo, da se vrednost
osi pomikamo v smeri večjih vrednosti in opazimo, da se vrednost 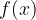 funkcije zmanjšuje, potem funkcija pada:
funkcije zmanjšuje, potem funkcija pada:
Če v določenem intervalu za vsak par neodvisnih spremenljivk 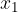 in
in 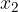 velja
velja
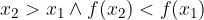
je v tem intervalu funkcija 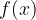 padajoča.
padajoča.
Če pa se po  osi pomikamo v smeri večjih vrednosti in ne opazimo spremembe vrednosti funkcije
osi pomikamo v smeri večjih vrednosti in ne opazimo spremembe vrednosti funkcije 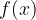 , je funkcija konstantna:
, je funkcija konstantna:
Če v določenem intervalu za vsak par neodvisnih spremenljivk 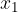 in
in 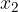 velja
velja
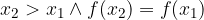
je v tem intervalu funkcija 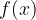 konstantna.
konstantna.
Za graf funkcije velja:
Na intervalu, kjer je vrednost funkcije narašča, se z večanjem neodvisne spremenljivke  graf funkcije vzpenja glede na ordinatno os.
graf funkcije vzpenja glede na ordinatno os.
Na intervalu, kjer je vrednost funkcije pada, se z večanjem neodvisne spremenljivke  graf funkcije spušča glede na ordinatno os.
graf funkcije spušča glede na ordinatno os.
V točkah, kjer je vrednost funkcije konstanta, je graf funkcije vodoraven oziroma vzporeden z abscisno osjo.
Računsko ugotavljanje intervala naraščanja in padanja presega nivo tega gradiva in se ga lotimo kasneje v gradivu Uporaba odvoda.
Funkcija je lahko omejena bodisi navzgor ali navzdol, lahko pa je tudi neomejena.
Če obstaja največja vrednost funkcije v okviru definicijskega območja, je funkcija omejena navzgor:
Če za vse  v definicijskem območju funkcije
v definicijskem območju funkcije 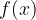 velja
velja
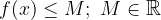
je funkcija 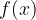 navzgor omejena.
navzgor omejena.
Če obstaja najmanjša vrednost funkcije v okviru definicijskega območja, je funkcija omejena navzdol:
Če za vse  v definicijskem območju funkcije
v definicijskem območju funkcije 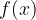 velja
velja
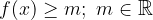
je funkcija 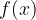 navzdol omejena.
navzdol omejena.
Če ne obstaja niti najmanjša, niti največja vrednost funkcije v okviru definicijskega območja, funkcija ni omejena.
Za graf funkcije velja:
Graf navzgor omejene funkcije doseže najvišjo točko glede na ordinatno os.
Graf navzdol omejene funkcije doseže najnižjo točko glede na ordinatno os.
Če v funkcijo vstavimo poljubni nasprotni vrednosti neodvisne spremenljivke  in dobimo v obeh primerih enako vrednost odvisne spremenljivke
in dobimo v obeh primerih enako vrednost odvisne spremenljivke 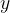 , je funkcija soda.
, je funkcija soda.
Funkcija  je soda, če za vsak
je soda, če za vsak  znotraj definicijskega območja funkcije velja
znotraj definicijskega območja funkcije velja 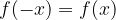
Če v funkcijo vstavimo poljubni nasprotni vrednosti neodvisne spremenljivke  in dobimo za rezultat nasprotni vrednosti odvisne spremenljivke
in dobimo za rezultat nasprotni vrednosti odvisne spremenljivke 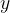 , je funkcija soda.
, je funkcija soda.
Funkcija  je liha, če za vsak
je liha, če za vsak  znotraj definicijskega območja funkcije velja
znotraj definicijskega območja funkcije velja 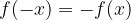
Računsko sodost in lihost določimo s preoblikovanjem predpisa funkcije.
Graf sode funkcije je simetričen glede na ordinatno os.
Graf lihe funkcije je simetričen glede na koordinatno izhodišče.
Injektivnost, surjektivnost in bijektivnost so lastnosti funkcije. Oglejmo si jih.
Funkcija je injektivna, če preslika različne originale v različne slike.
Injektivnost v grafu preverimo tako, da narišemo vzporednice k abscisni osi. V primeru, ko je funkcija injektivna, vsaka taka vzporednica seka graf le v eni točki. Če premica graf seka v dveh (ali več) točkah, potem funkcija ni injektivna.
Funkcija je surjektivna, če je njena zaloga vrednosti enaka množici 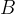 . Z drugimi besedami to pomeni, če je vsak element iz množice
. Z drugimi besedami to pomeni, če je vsak element iz množice 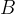 slika vsaj enemu elementu iz množice
slika vsaj enemu elementu iz množice 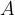 .
.
Če je funkcija injektivna in surjektivna hkrati, pravimo, da je funkcija bijektivna. Z drugimi besedami to pomeni, da je vsak element iz množice 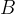 slika natanko enega elementa iz množice
slika natanko enega elementa iz množice 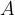 .
.