Osebne zbirke


Naj bo dan pravokotni trikotnik:
Funkciji sinus in kosinus v pravokotnem trikotniku povezujeta ostri kot in kateti trikotnika:
Funkcija sinus kota 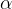 je definirana kot razmerje med nasprotiležno stranico (a) in hipotenuzo (c):
je definirana kot razmerje med nasprotiležno stranico (a) in hipotenuzo (c):
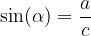
Funkcija kosinus kota 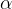 je definirana kot razmerje med priležno stranico (b) in hipotenuzo (c):
je definirana kot razmerje med priležno stranico (b) in hipotenuzo (c):
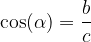
V naslednjih poglavjih bomo spoznali, da sta funkciji sinus in kosinus enaki, s to razliko da sta zamaknjeni za natanko 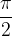 . Iz tega sledi, da bodo za
. Iz tega sledi, da bodo za 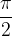 zamaknjene tudi:
zamaknjene tudi:
ničle
maksimumi
minimumi
Iz Pitagorovega izreka izpeljimo zvezo med sinusom in kosinusom. Pri tem po zgornji skici povzemimo oznake stranic pravokotnega trikotnika.
Pitagorov izrek izražen na enotski krožnici s funkcijama sinus in kosinus:
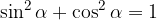
Narišimo funkciji sinus in kosinus na enotsko krožnico:
Z risanjem funkcij na enotsko krožnico poenostavimo obravnavo obeh funkcij; vrednost hipotenuze c je enaka 1, s tem pa se nam enačbi za sinus in kosinus poenostavita v:
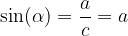
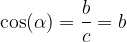
Vrednosti lahko ponazorimo na enotski krožnici:
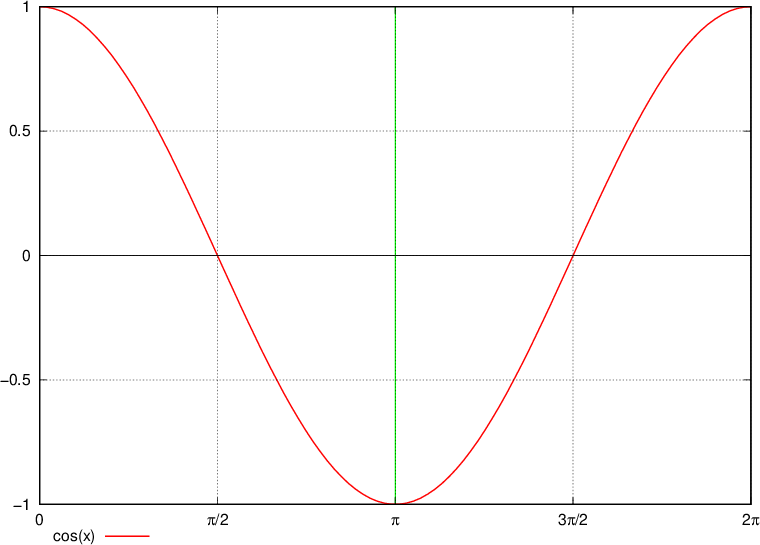
Narišimo funkciji sinus in kosinus. Na x os vnašamo vrednosti kota  , na y os pa vrednost sinusa.
, na y os pa vrednost sinusa.
Vrednost kota  se izraža v radianih. To pomeni, da je vrednost
se izraža v radianih. To pomeni, da je vrednost  enaka 3,14159... in ne 180°.
enaka 3,14159... in ne 180°.
Pri risanju sinusne funkcije kot 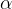 nanašamo na x os. Zato, ko obravnavamo graf, namesto oznake
nanašamo na x os. Zato, ko obravnavamo graf, namesto oznake 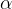 , uporabimo za kot oznako x.
, uporabimo za kot oznako x.
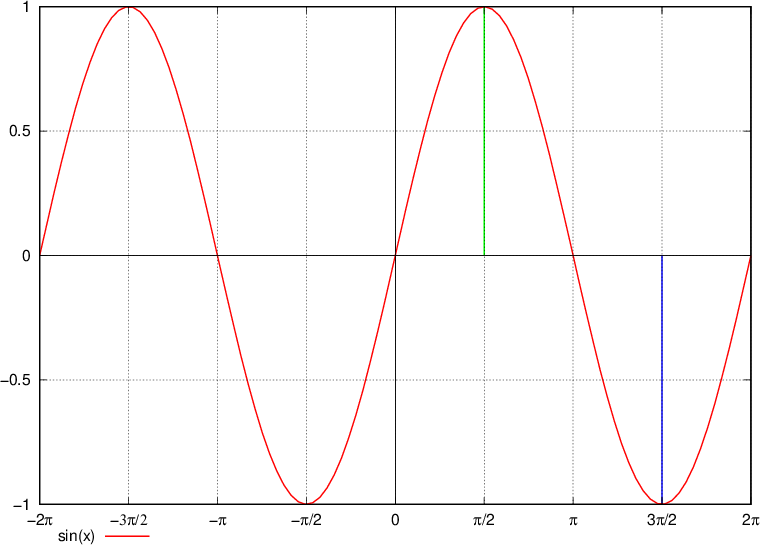
Graf osnovnega sinusa
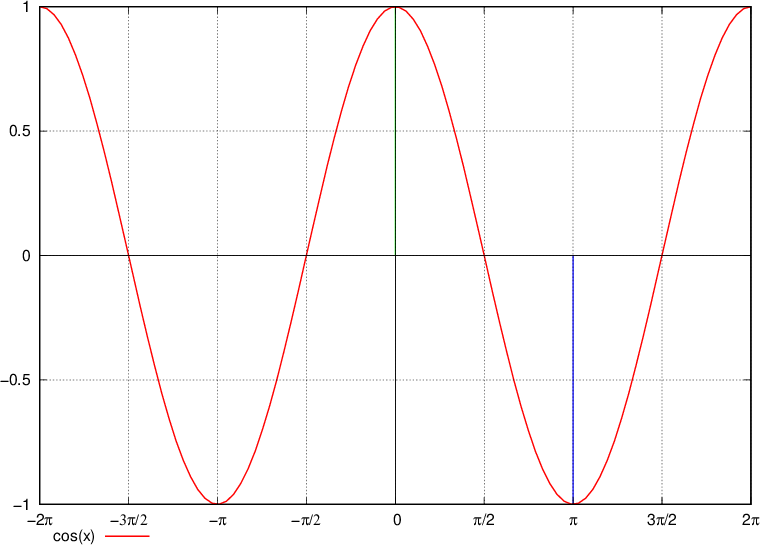
Graf osnovnega kosinusa
V definicijsko območje 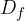 spadajo vsi tisti
spadajo vsi tisti 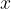 , ki jih lahko narišemo na graf. Tako za sinus in kosinus je definicijsko območje obeh funkcij celotna realna os oziroma: katerikoli kot si izberemo, za čisto vsakega bo funkcija obstajala.
, ki jih lahko narišemo na graf. Tako za sinus in kosinus je definicijsko območje obeh funkcij celotna realna os oziroma: katerikoli kot si izberemo, za čisto vsakega bo funkcija obstajala.
Definicijsko območje funkcije sinus in kosinus je celotna realna množica:
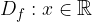
V zalogo vrednosti spadajo vsi tisti y, ki se pojavijo na grafu. Iz grafa za sinus in kosinus na enotski krožnici lahko opazimo, da je zaloga vrednosti 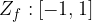 .
.
Zaloga vrednosti funkcije sinus in kosinus na enotski krožnici:
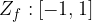
Zaloga vrednosti nam pove, da sta funkciji omejeni; funkciji na enotski krožnici sta omejeni med 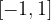 .
.
Ničle funkcije so tiste točke, kjer funkcija seka x os.
Ničle sinusa dobimo pri vsakem večkratniku 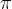 , oziroma, funkcija sinus ima vrednost nič za kote:
, oziroma, funkcija sinus ima vrednost nič za kote:
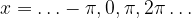
oziroma, drugače povedano:
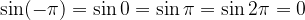
Ničle sinusa dobimo z nastavkom:
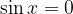
Rešitev nastavka je:
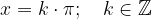
Ničle kosinusa dobimo pri vsakem večkratniku 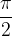 , oziroma, kosinus ima vrednost nič za kote:
, oziroma, kosinus ima vrednost nič za kote:
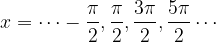
oziroma, drugače povedano:
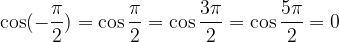
Ničle kosinusa dobimo z nastavkom:
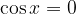
Rešitev nastavka je:
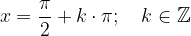
Maksimumi funkcij sinus in kosinus so tiste točke, kjer funkcija doseže največjo vrednost na y osi. Minimumi pa tisti, kjer funkciji dosežeta najnižjo vrednost na y osi.
Maksimumi funkcije nastopajo (glej graf) pri:
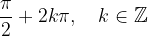
Maksimume sinusa dobimo z nastavkom:
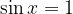
Rešitev nastavka je:
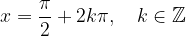
Minimumi funkcije nastopajo (glej graf) pri:
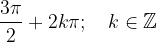
Minimume sinusa dobimo z nastavkom:
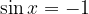
Rešitev nastavka je:
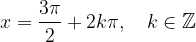
Maksimumi funkcije nastopajo (glej graf) pri:
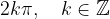
Maksimume kosinusa dobimo z nastavkom:
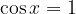
Rešitev nastavka je:
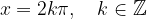
Minimumi funkcije nastopajo (glej graf) pri:
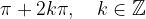
Minimume kosinusa dobimo z nastavkom:
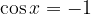
Rešitev nastavka je:
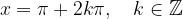
Funkcija je liha, če je simetrična glede na koordinatno izhodišče, oziroma:
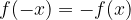
Funkcija je soda, je simetrična glede na y os:
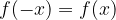
Za funkcijo sinus velja:
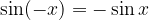
kar lahko preverimo tudi na grafu. Očitno je funkcija sinus liha.
Za funkcijo kosinus velja:
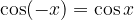
kar lahko preverimo tudi na grafu. Očitno je funkcija kosinus soda.
Naraščanje in padanje sinusa je iz grafa zelo enostavno razbrati:
sinus narašča do zelene črte oziroma od 0 pa do 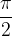
sinus pada od zelene pa do modre črte oziroma od 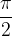 pa do
pa do 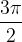
ter spet pada od modre črte naprej oziroma od 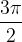 pa do
pa do 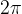
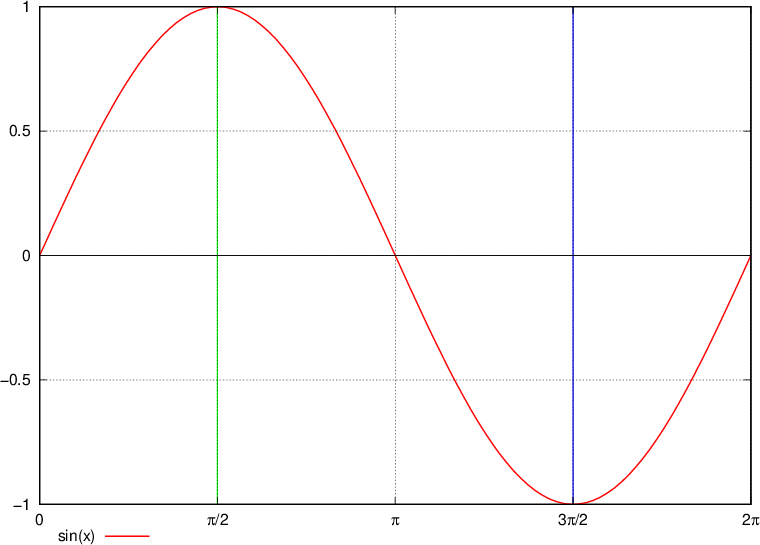
Naraščanje in padanje kosinusa prav tako enostavno razberemo:
kosinus pada do zelene črte oziroma od 0 pa do 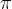
kosinus narašča od zelene naprej 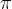 pa do
pa do 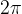
Obe funkciji sta periodični s periodo 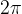 . Vse vrednosti (razen ničel, ki se ponavljajo na vsakih
. Vse vrednosti (razen ničel, ki se ponavljajo na vsakih 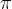 ) se na enotski krožnici (ali grafu) ponovijo na vsakih
) se na enotski krožnici (ali grafu) ponovijo na vsakih 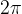 .
.
Velja:
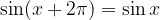
in
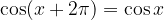
Funkciji sta zvezni na celotnem definicijskem območju, torej povsod. Oziroma povedano drugače, grafa funkcij se nikjer ne 'pretrgata'.