Osebne zbirke


Naj bo dan pravokotni trikotnik:
Funkciji tangens in kotangens v pravokotnem trikotniku povezujeta ostri kot in kateti trikotnika:
Funkcija tangens kota 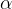 je definirana kot razmerje med nasprotiležno stranico (a) in priležno stranico (b):
je definirana kot razmerje med nasprotiležno stranico (a) in priležno stranico (b):
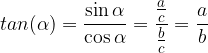
Funkcija kotangens kota 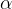 je definirana kot razmerje med priležno stranico (b) in nasprotiležno stranico (a):
je definirana kot razmerje med priležno stranico (b) in nasprotiležno stranico (a):
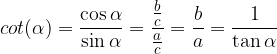
Narišimo funkciji tangens in kotangens na enotsko krožnico:
Vrednosti tangensa in kotangensa je z enotske krožnice nekoliko težje brati, zato si bomo za risanje pomagali z vrednostmi sinusa in kosinusa, ki jih že poznamo (tabelo bomo samo razširili in izračunali vrednosti od 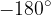 do
do 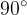 ), nam bo veliko lažje narisati tangens in kotangens s pomočjo teh vrednosti.
), nam bo veliko lažje narisati tangens in kotangens s pomočjo teh vrednosti.
Za izračun tangensa in kotangensa uporabimo formuli:
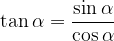
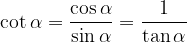
Vrednost kota α se izraža v radianih. To pomeni, da je vrednost π enaka 3.14159... in ne 180°.
Narišimo funkcijo tangens. Na x os vnašamo vrednosti kota α, na y os pa vrednost tangensa:
Pri risanju funkcije tangens kot α nanašamo na x os. Zato, ko obravnavamo graf, namesto oznake α, uporabimo za kot oznako x.
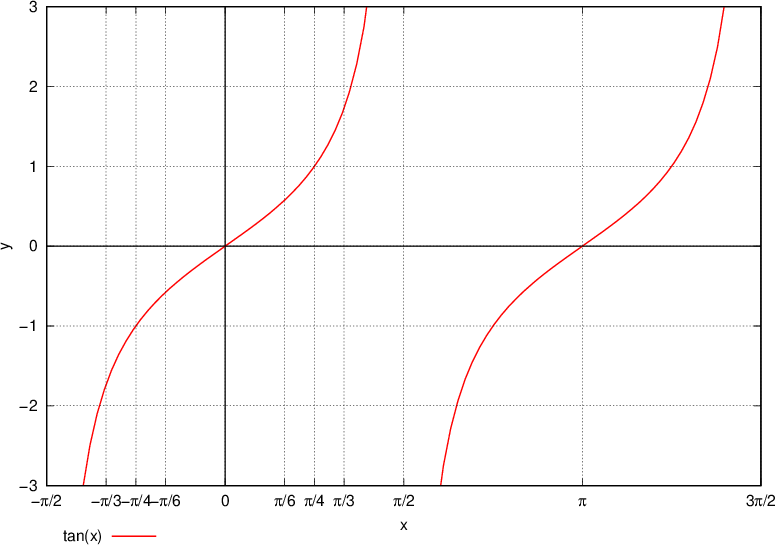
Odčitavamo vrednosti iz tabele in jih primerjamo z grafom - vrednosti morajo biti enake:
Začnemo z odčitavanjem vrednosti v tabeli s kotom 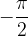 in dobimo vrednost
in dobimo vrednost 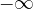 .
.
naslednja vrednost α, ki jo obravnavamo, je enaka  , preberemo vrednost
, preberemo vrednost 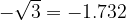 .
.
nadaljujemo s kotom 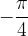 , preberemo vrednost tangensa
, preberemo vrednost tangensa 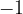 .
.
pri kotu 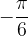 preberemo vrednost
preberemo vrednost 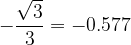 .
.
pri kotu 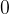 preberemo vrednost tangensa
preberemo vrednost tangensa 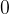 .
.
ko je kot α enak 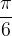 , preberemo v tabeli vrednost funkcije tangens, ki je enaka
, preberemo v tabeli vrednost funkcije tangens, ki je enaka 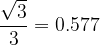 .
.
ko kot α na enotski krožnici povečamo na 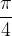 , tangens doseže vrednost
, tangens doseže vrednost 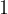 .
.
ko povečamo kot α na 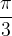 , odčitamo vrednost tangensa
, odčitamo vrednost tangensa 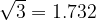 .
.
povečajmo kot α na 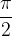 , odčitamo vrednost tangensa
, odčitamo vrednost tangensa 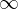 , od tukaj naprej se začnejo vrednosti ponavljati, lahko zaključimo, da se tangens ponavlja na vsakih
, od tukaj naprej se začnejo vrednosti ponavljati, lahko zaključimo, da se tangens ponavlja na vsakih 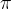 .
.
Naredili smo en krog po tabeli; če naredimo nov krog, se bodo vsi koraki ponovili. Očitno je, da se bo funkcija ponovila na razmikih 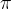 .
.
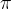 je zato perioda funkcije.
je zato perioda funkcije.
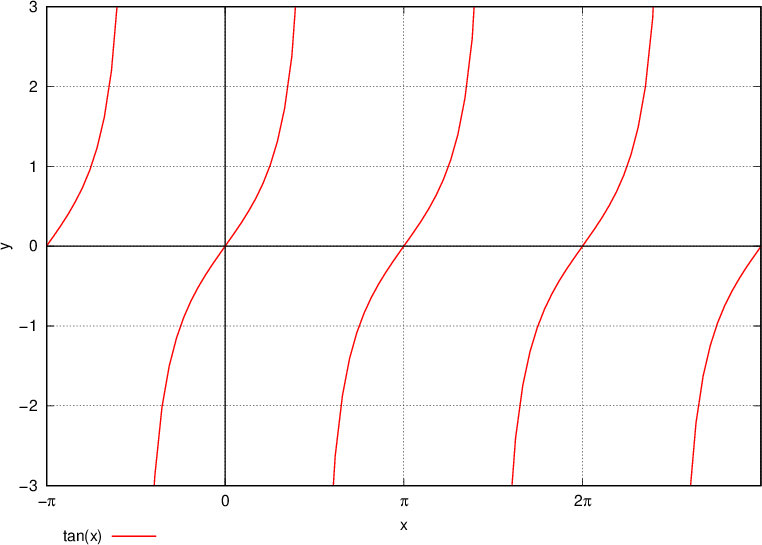
Funkcija tangens je periodična s periodo 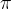 . Na grafu lahko periodičnost / ponavljanje zlahka opazimo.
. Na grafu lahko periodičnost / ponavljanje zlahka opazimo.
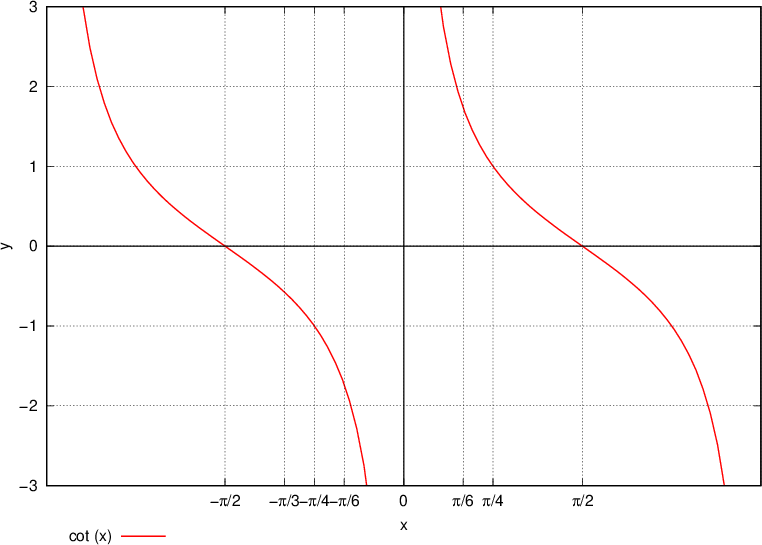
Postopek se pri kotangensu ponovi - odčitavamo vrednosti iz tabele in jih primerjamo z grafom - vrednosti morajo biti enake.
Začnemo z odčitavanjem vrednosti v tabeli s kotom 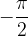 in dobimo vrednost
in dobimo vrednost 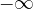 .
.
Naslednja vrednost α, ki jo obravnavamo, je enaka 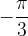 , preberemo vrednost
, preberemo vrednost 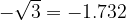 .
.
Nadaljujemo s kotom 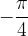 , preberemo vrednost kotangensa
, preberemo vrednost kotangensa 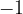 .
.
Pri kotu 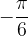 preberemo vrednost
preberemo vrednost 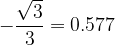 .
.
Pri kotu 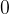 preberemo vrednost kotangensa
preberemo vrednost kotangensa 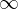 .
.
Ko je kot α enak 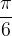 , preberemo v tabeli vrednost funkcije kotangens, ki je enaka
, preberemo v tabeli vrednost funkcije kotangens, ki je enaka 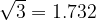 .
.
Ko kot α na enotski krožnici povečamo na 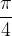 , kotangens doseže vrednost
, kotangens doseže vrednost 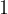 .
.
Ko povečamo kot α na 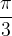 , odčitamo vrednost kotangensa
, odčitamo vrednost kotangensa 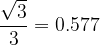 .
.
Povečajmo kot α na 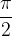 , odčitamo vrednost kotangensa 0
, odčitamo vrednost kotangensa 0 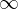 , od tukaj naprej se začnejo vrednosti ponavljati, lahko zaključimo, da se kotangens ponavlja na vsakih
, od tukaj naprej se začnejo vrednosti ponavljati, lahko zaključimo, da se kotangens ponavlja na vsakih 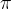 .
.
Naredili smo en krog po tabeli; če naredimo nov krog, se bodo vsi koraki ponovili. Očitno je, da se bo funkcija ponovila na razmikih 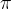 .
.
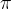 je zato perioda funkcije.
je zato perioda funkcije.
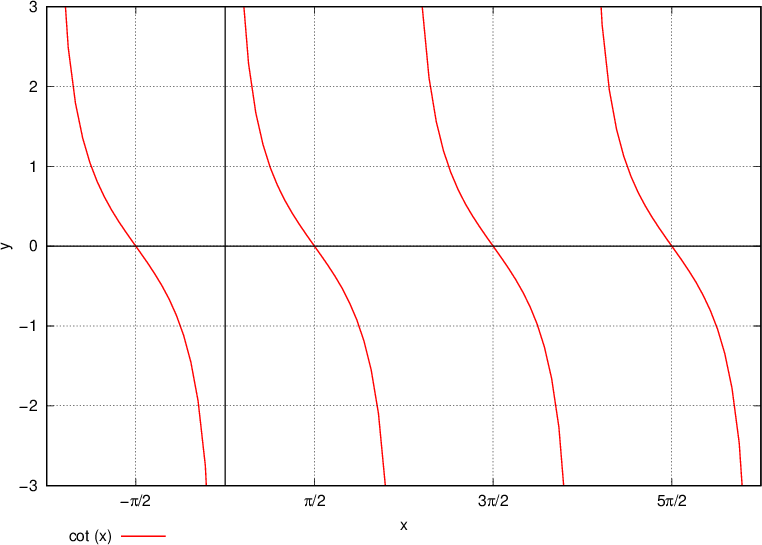
Funkcija kotangens je periodična s periodo 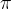 . Na grafu lahko periodičnost / ponavljanje zlahka opazimo.
. Na grafu lahko periodičnost / ponavljanje zlahka opazimo.
Lastnosti obeh funkcij najlažje odčitamo z grafa. V nadaljevanju bomo lastnosti, ki smo jih spoznali prek grafa, opisali še na matematični način.
V definicijsko območje 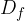 spadajo vsi tisti x, ki jih lahko narišemo na graf in za te x-e funkcija obstaja.
spadajo vsi tisti x, ki jih lahko narišemo na graf in za te x-e funkcija obstaja.
Tangens in kotangens sta definirana kot ulomka (glej uvod v gradivo). Vemo, da ulomek ne more obstajati (ni definiran), če je imenovalec enak 0, torej bomo iz definicijskega območja izvzeli vse tiste vrednosti funkcij, pri katerih dobimo vrednost imenovalca 0. Te vrednosti imenujemo poli ali navpične asimptote.
V zalogo vrednosti spadajo vsi tisti y, ki se pojavijo na grafu.
Funkcija tangens je definirana kot
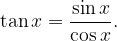
Tangens ima pole natančno takrat, ko je 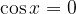 (ničle kosinusa), to pa je pri vsakem
(ničle kosinusa), to pa je pri vsakem
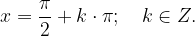
Definicijsko območje funkcije tangens je celotna realna os x brez  , oziroma:
, oziroma:
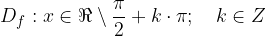
Iz grafa tangens funkcije in v tabeli lahko opazimo, da je zaloga vrednosti 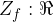 .
.
Zaloga vrednosti funkcije tangens:
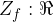
Funkcija kotangens je definirana kot
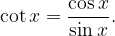
Kotangens ima pole natančno takrat, ko je 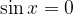 (ničle sinusa), to pa je pri vsakem
(ničle sinusa), to pa je pri vsakem
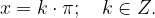
Definicijsko območje funkcije kotangens je celotna realna os x brez 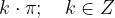 .
.
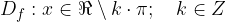
V zalogo vrednosti spadajo vsi tisti y, ki se pojavijo na grafu. Iz grafa kotangens funkcije in v tabeli lahko opazimo, da je zaloga vrednosti 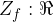 .
.
Zaloga vrednosti funkcije kotangens:
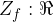
Ničle funkcije so tiste točke, kjer funkcija seka x os.
Ničle tangensa dobimo pri vsakem večkratniku 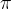 , oziroma, funkcija tangens ima vrednost nič za kote:
, oziroma, funkcija tangens ima vrednost nič za kote:
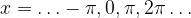
oziroma, drugače povedano:
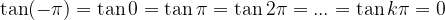
Ničle tangensa dobimo z nastavkom:
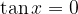
Rešitev nastavka je:
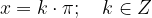
Ničle kotangensa dobimo pri vsakem večkratniku 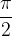 (pri ničlah kosinusa).
(pri ničlah kosinusa).
oziroma, drugače povedano:
Ničle kotangensa dobimo z nastavkom:
Rešitev nastavka je:
Pole tangensa dobimo pri vsakem večkratniku 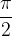 (pri ničlah kosinusa), oziroma, tangens pri teh vrednostih ne obstaja (ni definiran).
(pri ničlah kosinusa), oziroma, tangens pri teh vrednostih ne obstaja (ni definiran).
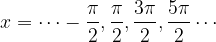
oziroma, drugače povedano:
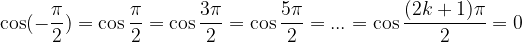
Pole tangensa dobimo z nastavkom:
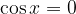
Rešitev nastavka je:
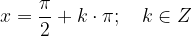
Pole kotangensa dobimo pri vsakem večkratniku 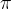 (ničle sinusa):
(ničle sinusa):
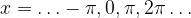
oziroma, drugače povedano:
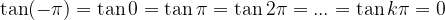
Pole kotangensa dobimo z nastavkom:
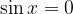
Rešitev nastavka je:
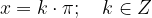
Funkcija je liha, če je simetrična glede na koordinatno izhodišče, oziroma:
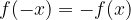
Funkcija je soda, če je simetrična glede na y os:
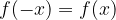
Za funkcijo tangens velja:
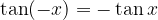
kar lahko razberemo tudi z grafa (funkcija je simetrična glede na koordinatno izhodišče). Očitno je funkcija tangens liha.
Za funkcijo kotangens velja:
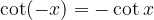
kar lahko razberemo tudi z grafa (funkcija je simetrična glede na koordinatno izhodišče). Očitno je funkcija kotangens liha.
Naraščanje tangensa je iz grafa zelo enostavno razbrati. Funkcija narašča na celotnem  .
.
Tudi padanje kotangensa enostavno razberemo. Kotangens pada na celotnem  .
.
Zaloga vrednosti obeh funkcij nam pove, da sta funkciji neomejeni.
Funkciji tangens in kotangens sta periodični s periodo 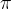 . Na grafu lahko periodičnost / ponavljanje zlahka opazimo.
. Na grafu lahko periodičnost / ponavljanje zlahka opazimo.
Velja:
Funkcija tangens se na vsakih 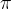 ponavlja.
ponavlja.
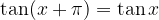
in
Funkcija kotangens se na vsakih 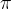 ponavlja.
ponavlja.
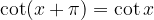
Funkciji tangens in kotangens sta nezvezni. Na grafu se to razbere, kjer se ''pretrgata'' v polih.