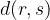Osebne zbirke


Ravnina je neskončno velika in neskončno tanka ravna ploskev, ki se razteza v dveh smereh.
Ravnina je neomejena ravna ploskev, ki ima dve razsežnosti:
dolžino in
širino.
Označimo jo z veliko pisano črko 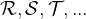
Spoznali bomo osnovne geometrijske elemente v ravnini:
točko
premico
poltrak in
daljico
ter njihove lastnosti, medsebojne odnose in lege.
Medsebojne odnose bomo zapisali tudi z matematičnimi simboli.
Točka je najmanjši element v ravnini. Vsi ostali geometrijski elementi in liki so sestavljeni iz množice točk.
Točke označujemo z velikimi tiskanimi črkami 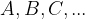
V ravnini dve točki lahko bodisi:
Sovpadata - sta na istem mestu
Sovpadanje točk A in B v ravnini z matematičnimi simboli zapišemo z znakom enakosti:
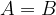
Ne sovpadata
Točki A in B, ki v ravnini ne sovpadata, z matematičnimi simboli zapišemo z znakom za neenakost:
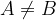
Premica je neomejena ravna črta, sestavljena iz neskončnega števila točk.
Premico označimo z malo tiskano črko 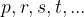
Točka in premica sta v ravnini lahko v naslednjem odnosu:
Točka leži na premici
Točko A, ki leži na premici p, z matematičnimi simboli zapišemo z znakom:
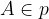
Točka ne leži na premici
Točko A, ki ne leži na premici p, z matematičnimi simboli zapišemo kot:
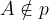
Odnos dveh premic v ravnini pa je lahko naslednji:
Premici sta vzporedni
Vzporedni premici nimata nobene skupne točke - se ne sekata.
Vzporednost premic p in q v ravnini z matematičnimi simboli zapišemo kot:
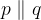
Premici se sekata
Premici sečnici imata natanko eno skupno točko.
Premici p in q, ki se sekata v točki A, z matematičnimi simboli zapišemo kot:
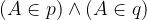
Gornji zapis preberemo kot: Točka A leži na premici p in A leži na premici q.
Enakovredno lahko ta odnos zapišemo tudi tako:
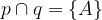
Gornji zapis preberemo kot: Presek premic p in q je točka A.
Če premici sečnici oklepata kot 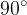 , sta pravokotni.
, sta pravokotni.
Premici p in q, ki se sekata pod pravim kotom, z matematičnimi simboli zapišemo kot:
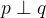
Premici sovpadata
Premici, ki sovpadata, imata neskončno skupnih točk.
Premici p in q, ki v ravnini sovpadata, z matematičnimi simboli zapišemo kot:
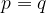
Poltrak je ravna črta, ki je na eni strani neomejena, na drugi strani pa jo omejuje točka. To točko imenujemo izhodišče poltraka.
Poltrak označimo z malo tiskano črko  Izhodišče pa z veliko tiskano črko
Izhodišče pa z veliko tiskano črko 
Daljica je ravna črta, ki je na obeh konceh omejena s točkama. Ti dve točki imenujemo krajišči daljice.
Daljico označimo s parom velikih tiskanih črk, ki označujeta krajišči daljice 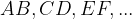
Daljici lahko določimo dolžino. Dolžina daljice je najkrajša razdalja med krajišči daljice.
Dolžino daljice s krajiščema A in B z matematičnimi simboli zapišemo kot:
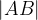
Velja, da je dolžina daljice s krajišči A in B enaka razdalji med točkama A in B, kar z matematičnimi simboli zapišemo kot:
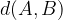
Za dolžino daljice torej lahko enakovredno uporabljamo oba zapisa.
Dve daljici sta skladni, če imata enako dolžino.
Razdalja med točko in premico predstavlja najkrajšo razdaljo med njima, to je pravokotno na premico.
Razdalja med točko T in premico p je odsek pravokotnice q med točko T in presečiščem premic p in q. Z matematičnimi simboli razdaljo med točko T in premico p zapišemo kot:
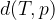
Razdaljo med premicama določimo le, če sta ti vzporedni. Sicer pa se premici sekata in je razdalja med njima enaka 0.
Razdalja med premicama predstavlja najkrajšo razdaljo med njima, to je pravokotno na obe premici.
Razdalja med premicama r in s je odsek pravokotnice t med presečišči le-te s premicama r in s. Z matematičnimi simboli razdaljo med premicama r in s zapišemo kot: