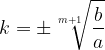Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Zaporedje je geometrijsko, če je količnik poljubnih dveh zaporednih členov konstanten. Vsak naslednji člen zaporedja izračunamo tako, da prejšnjega pomnožimo z istim številom.
Zapišimo nekaj zaporednih členov geometrijskega zaporedja, pri čemer količnik dveh zaporednih členov označimo s k, prvi člen zaporedja pa z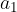 
.
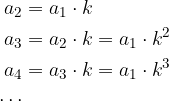
Zapišimo splošni člen geometrijskega zaporedja:
Obrazec za splošni člen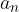 
geometrijskega zaporedja, kjer 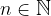je 
, je:
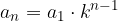
Velja, da je splošni člen geometrijskega zaporedja eksponentna funkcija spremenljivke n.
Količnik dveh zaporednih členov imenujemo količnik geometrijskega zaporedja, označimo ga s k. Količnik je vedno konstanten.
Obrazec za količnik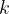 
geometrijskega zaporedja, kjer 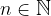je , je:
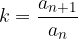
oziroma:
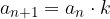
Naraščanje in padanje geometrijskega zaporedja je odvisno od prvega člena 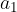in količnika zaporedja k.
Velja:
Vsak člen geometrijskega zaporedja s samimi pozitivnimi členi, z izjemo prvega, je enak geometrijski sredini svojih sosedov.
Geometrijska sredina poljubnih dveh pozitivnih števil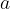 
in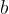 
je število:
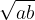
Geometrijska sredina dveh poljubnih simetrično ležečih členov zaporedja pa je člen:
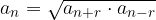
Geometrijska sredina dveh pozitivnih števil 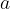in 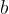je manjša ali enaka aritmetični sredini istih dveh števil:
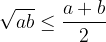
Poglejmo kako lahko to dokažemo računsko. Vemo, da za poljubni števili 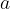in 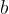vedno velja naslednja trditev:
Za neenačbo (1) velja, da bo njena vrednost vedno pozitivna oziroma enaka 0 le, če velja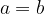 
. S pomočjo neenačbe (1) dokažimo povezavo med geometrijsko in aritmetično sredino:
Poglejmo si še grafični dokaz. Pomagamo si z lastnostmi kota v polkrogu in višinskega izreka v pravokotnem trikotniku (glej Slika 1).
Nad daljico dolžine a + b narišemo polkrog in v polkrog vrišemo dva trikotnika. Zelo hitro lahko opazimo, da je aritmetična sredina 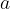in ,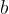 
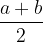ravno polmer kroga, ki je hkrati višina prvega trikotnika.
Kaj pa višina drugega trikotnika? Po višinskem izreku v pravokotnem trikotniku je višina na hipotenuzo - premer polkroga - enaka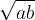 
. To pa je ravno geometrijska sredina števil 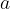in .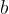
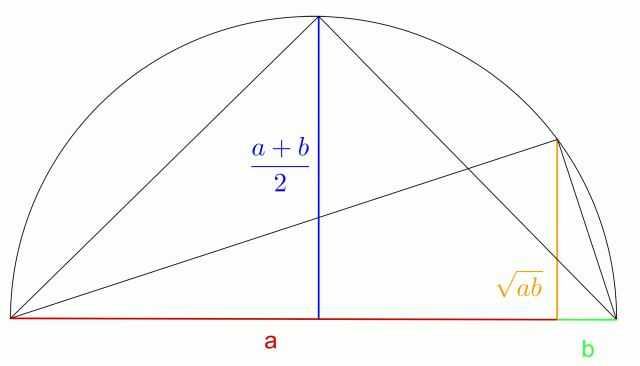
Slika 1: očitno je, da je geometrijska sredina manjša od aritmetične in enaka le v primeru, ko sta števili 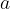in 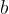enaki.
Imejmo števili 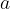in 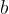in denimo, da želimo med ti dve števili vriniti m števil tako, da števila 
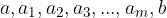tvorijo končno geometrijsko zaporedje. Ta postopek imenujemo geometrijska interpolacija.
Z geometrijsko interpolacijo dobimo geometrijsko zaporedje, za katero velja, da je sestavljeno iz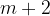 
členov, prvi člen 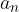je enak a in zadnji člen 
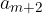je enak b.
Poiščimo obrazec za izračun količnika tako dobljenega geometrijskega zaporedja:
Obrazec za količnik geometrijskega zaporedja, ki ga dobimo s postopkom geometrijske interpolacije, ko med števili 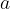in 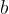vrinemo 
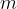števil, je:
