Osebne zbirke


Graf linearne funkcije 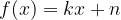 je premica z enačbo
je premica z enačbo
kjer sta k in n iz množice realnih števil.
Začetna vrednost vsake funkcije je točka v x = 0. Začetno vrednost v splošnem zapišemo:
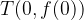
V primeru linearne funkcije za f(0) vstavimo
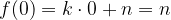
in dobimo začetno vrednost linearne funkcije:
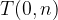
Če je n = 0, gre premica skozi točko 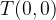 , ki jo imenujemo koordinatno izhodišče.
, ki jo imenujemo koordinatno izhodišče.
Število k imenujemo na dva načina.
Največkrat ga imenujemo smerni koeficient, saj določa smer.
Ker pa je k razmerje med spremembo vrednosti funkcije y in spremembo spremenjljivke x, ga imenujemo tudi diferenčni kvocient.
Če poznamo koordinati dveh točk 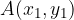 in
in 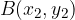 skozi kateri poteka premica z enačbo
skozi kateri poteka premica z enačbo 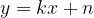 , lahko izračunamo smerni kooeficient premice.
, lahko izračunamo smerni kooeficient premice.
Diferenčni kvocient izračunamo tako, da v isto linerano funkcijo vstavimo dve različni točki:
Naj bosta dani dve točki, 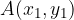 in
in 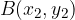 . Smerni koeficient premice, ki poteka skozi ti dve točki, izračunamo s formulo:
. Smerni koeficient premice, ki poteka skozi ti dve točki, izračunamo s formulo:
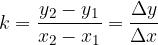
Premice, ki imajo enak smerni koeficient k, so med seboj vzporedne.
Premice s smernim koeficientom k = 1 naraščajo in so vzporedne simetrali lihih kvadrantom z enačbo y = x. Premice z abscisno osjo oklepajo kot 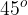 .
.
Funkcija je naraščajoča v primeru, ko za poljubna originala 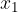 in
in 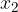 velja, da če
velja, da če
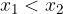
potem nujno:
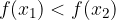
Če je k negativno število, je funkcija padajoča. Premice z abscisno osjo oklepajo kot večji od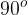 .
.
Funkcija je konstantna, ko je k = 0. Dokaz:
Enačba premice je tako enaka 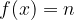 in se z vrednostjo x ne spreminja. Graf te funkcije je vzporeden z abscisno osjo.
in se z vrednostjo x ne spreminja. Graf te funkcije je vzporeden z abscisno osjo.
Po definiciji je ničla funkcije tisto število 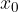 , ko velja:
, ko velja:
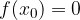
Graf funkcije v ničli seka abscisno os v točki 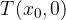 .
.
Oglejmo si postopek za iskanje ničle funkcije.
V primeru, da je k = 0 velja, da je graf funkcije je vzporeden z abscisno osjo; če
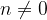 , potem graf funkcije nikoli ne seka x osi.
, potem graf funkcije nikoli ne seka x osi.
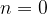 , potem je graf funkcije kar enak x osi oziroma abscisi.
, potem je graf funkcije kar enak x osi oziroma abscisi.
Graf lineane funkcije lahko narišemo na dva načina.
Prvi način je, da izračunamo dve točki in skozi obe točki narišemo premico.
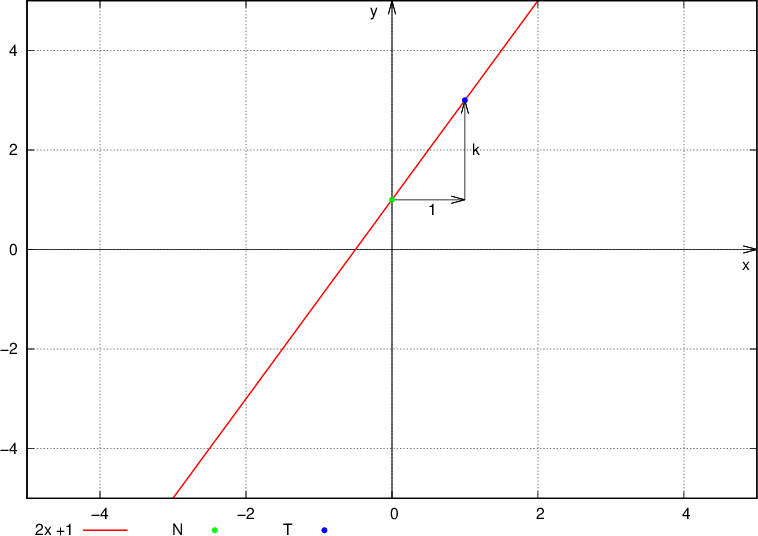
Drugi način je, da uporabimo postopek risanja linearne funkcije, kjer uporabimo podatka začetne vrednosti in smernega koeficienta premice.
Oglejmo si postopek:
narišemo točko na ordinatni osi s koordinatami 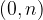 , kjer je n začetna vrednost,
, kjer je n začetna vrednost,
drugo točko narišemo tako, da se iz prve točke pomaknemo za eno enoto v desno in za k enot navzgor (oz. navzdol, če je k negativen),
skozi obe točki narišemo premico.
Poglejmo si še funkcijo absolutne vrednosti, katere graf ni premica.
Postopek risanja funkcije 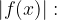
narišemo graf funkcije 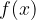
tisti del premice, ki je pod abscisno osjo, prezrcalimo čez abscisno os.
Poglejmo si primer.