Prijava z e-naslovom
Prijava brez gesla
Graf polinoma je nepretrgana krivulja, ki je definirana v celotnem območju realnih števil. Pri risanju grafa polinoma je potrebno poznati nekaj temeljnih podatkov:
začetno vrednost
ničle polinoma
obnašanje funkcije v neskončnosti
ekstreme funkcije
To je vrednost, v kateri graf polinoma seka os y. Začetno vrednost razberemo iz polinoma tako, da pogledamo prosti člen:
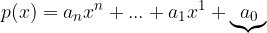
Začetna vrednost je točka, v kateri ima polinom vrednost prostega člena:
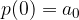
V ničlah graf polinoma križa ali pa se dotakne osi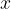 
.
Ničla polinoma je točka, kjer je vrednost polinoma enaka 0, torej:
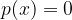
Postopek iskanja ničel je podrobneje razložen v poglavju Iskanje ničel polinoma. Poleg samih ničel je potrebno poznati tudi obnašanje polinoma v območju ob ničlah; polinom lahko namreč x os seka ali pa se je samo dotakne.
Pri izrisovanju grafa polinoma nas zanima, kaj se dogaja okoli posameznih ničel. Polinom se v določeni ničli lahko samo dotakne abscisne osi oziroma graf lahko prečka abscisno os in v tem primeru menja prednak.
Posamezne ničle so lahko enkratne ali večstopenjske ničle (se večkrat ponovijo). Prepoznamo dve vrsti ničel:
lihe ničle
sode ničle
Od stopnje ničle je odvisno, kako se obnaša graf v njihovi bližini.
V okolici ničel lihe stopnje graf spremeni predznak in torej prečka os x.
V okolici ničel sode stopnje graf polinoma ne spremeni predznaka, saj v ničli sode stopnje se polinom samo dotakne osi x.
Pri izrisovanju grafa polinoma nas zanima tudi obnašanje polinoma v skrajnostih. Podatek, ki ga iščemo je, ali pričemo z izrisovanjem na positivni strani ordinatne osi ali na negativni, oziroma ali naš graf zaključimo na pozitivni strani ali negativni. Obnašanje polinoma v neskončnosti je odvisno predvsem od vodilnega člena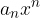 
, pri tem naš graf lahko:
začne pri negativnih vrednostih y in se konča v pozitivnih (narašča)
začne pri pozitivnih in se zaključi v negativnih vrednostih y (pada)
začne pri negativnih vrednostih y in se konča pri negativnih (konkavna)
začne pri pozitivnih in se zaključi v pozitivnih vrednostih y (konveksna)
Poglejmo, kako vodilni člen 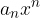vpliva na obnašanje grafa. Pri tem nas zanima, kje se graf prične (predznak) ne pa natančna vrednost:
ko gre 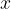proti neskončnosti 
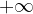, gledamo obnašanje grafa na desni strani.
ko gre 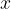proti minus neskončnosti 
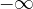, gledamo obnašanje grafa na levi strani.
Ko je vodilni člen lihe stopnje, se predznak grafa zamenja v neskončnosti. Če je koeficient večji od nič, potem graf narašča.
Ko je vodilni člen lihe stopnje, se predznak grafa zamenja v neskončnosti. Če je koeficient manjši od nič, potem graf pada.
Ko je vodilni člen sode stopnje, se predznak grafa ohranja. Če je koeficient večji od nič, potem se graf prične pri pozitivnih vrednostih in konča na pozitivnih vrednostih.
Ko je vodilni člen sode stopnje, se predznak grafa ohranja. Če je koeficient manjši od nič, potem se graf prične pri negativnih vrednostih in konča na negativnih vrednostih.
Za razumevanje tega poglavja je potrebno razumevanja poglavja Odvod.
Ekstremi so točke, v katerih funkcija naredi prevoj. Če v ekstremu postavimo tangento na graf polinoma, lahko vidimo, da je le-ta vzporedna z osjo x.
