Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Naj bosta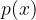 
in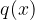 
dva polinoma. Če je 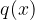neničelni polinom, je kvocient teh dveh polinomov racionalna funkcija:
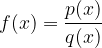
Ničle imenovalca imenujemo poli racionalne funkcije. V teh točkah racionalna funkcija ni definirana, definicijsko območje racionalne funkcije je zato množica realnih števil brez ničel imenovalca.
Ničle racionalne funckije 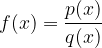so ničle števca racionalne funkcije (kjer je 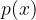enak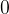 
).
Ničle racionalne funkcije 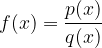poiščemo z enačbo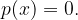 
Blizu ničle se graf racionalne funkcije obnaša podobno kot graf polinoma v števcu, torej podobno kot polinom .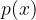
Če je ničla polinoma 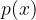sode stopnje, se graf racionalne funkcije v tej ničli dotakne abscisne osi in zato ne spremeni predznaka.
Če je ničla polinoma 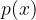lihe stopnje, graf racionalne funkcije v tej točke seka abscisno os in spremeni predznak.
Graf racionalne funkcije s sodo (levo) oziroma liho ničlo (desno).
Poli funkcije so ničle polinoma 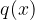, tj. imenovalca racionalne funkcije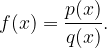 
Pole racionalne funkcije 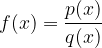poiščemo z enačbo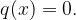 
V polih racionalna funkcija ni definirana, funkcija ima zato tam navpično asimptoto. Ko se približujemo polu, vrednosti funkcije ob asimptoti padajo ali rastejo pozitivno ali negativno v neskončnost.
Pol sode (levo) oziroma lihe stopnje (desno) racionalne funkcije.
Če je pol sode stopnje (ničla polinoma 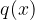je soda), funkcija pri prehodu čez pol ne spremeni predznaka.
Če je pol lihe stopnje (ničla polinoma 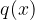je liha), funkcija pri prehodu čez pol spremeni predznak.
Če graf racionalne funkcije nima pola v x = 0, potem seka ordinatno os v neki točki T(0, n).
Če zapišemo polinoma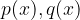 
v naslednji obliki:
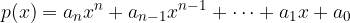
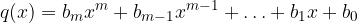
in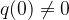 
, potem graf racionalne funkcije seka ordinatno os v:
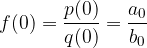
Vrednost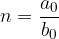 
je začetna vrednost te racionalne funkcije. Točka, v kateri graf seka ordinatno os, pa je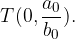 
Začetno vrednost funkcije 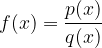poiščemo, tako da izračunamo 
.
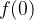Da bomo znali dovolj dobro narisati graf racionalne funkcije, poglejmo še kaj se dogaja z vrednostmi racionalne funkcije, ko gre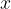 
čez vse meje. Videli bomo torej kako se obnaša racionalna funkcija daleč proč od izhodišča za zelo velike pozitivne (negativne) vrednosti .
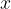Racionalna funkcija je kvocient dveh polinomov 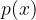in 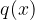. Vemo že, da se daleč od izhodišča (v neskončnosti) polinomi obnašajo kot vodilni člen tega polinoma.
Torej velja, da se vrednosti polinoma
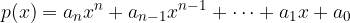
v neskončnosti, torej ko gre 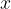proti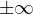 
obnašajo kot 
.
Vrednosti polinoma
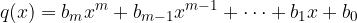
pa se v neskončnosti približujejo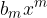 
.
Ker je racionalna funkcija kvocient dveh polinomov:
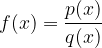
se v neskončnosti obnaša kot kvocient vodilnih členov:
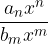
Ločimo tri različne možnosti:
Stopnja števca 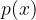je manjša od stopnje imenovalca .
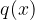Stopnja števca 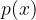je večja od stopnje imenovalca .
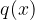Stopnja števca 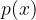je večja od stopnje imenovalca .
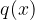Poglejmo si vsako možnost posebej!
Ko je stopnja števca manjša od stopnje imenovalca racionalne funkcije, se funkcija v neskončnosti približuje vodoravni asimptoti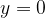 
, tj. abscisni osi.
Za polinoma:
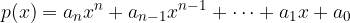
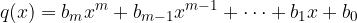
velja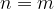 
.
Poglejmo si kvocient teh dveh polinomov:
Vrednosti vseh členov:
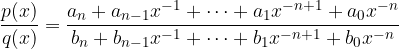
razen prostih členov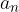 
in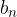 
, gredo z naraščajočim 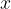proti .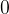
Naj bosta dana dva polinoma enakih stopenj:
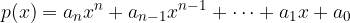
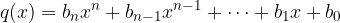
Graf racionalne funkcije se v tem primeru daleč proč od izhodišča približuje vodoravni asimptoti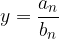 
, tj. proti količniku vodilnih koeficientov.
V primeru, ko je stopnja števca višja od stopnje imenovalca racionalne funkcije, polinom 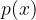delimo s polinomom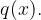 
Kvocient bo polinom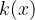 
, ostanek pa polinom 
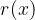nižje stopnje od delitelja 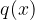. Polinom 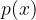zato lahko zapišemo takole:
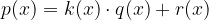
Če delimo polinom 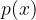s polinomom 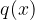, pa dobimo naslednjo enačbo:
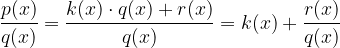
Graf racionalne funkcije
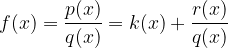
se daleč stran od izhodišča približuje krivulji 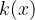, saj za velike 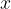gre vrednost kvocienta 
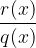proti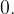 
Če je stopnja števca 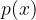višja od stopnje imenovalca 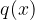, potem polinom 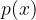delimo s polinomom .
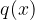Kvocient teh dveh polinomov 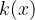bo krivulja, kateri se bo graf racionalne funkcije približeval daleč stran od koordinatnega izhodišča.
