Prijava z e-naslovom
Prijava brez gesla
Nihala lahko nihajo na več možnih načinov. V tem poglavju bomo obravnavali periodično nihanje, ko je odmik nihala od ravnovesne lege sinusna funkcija časa. Temu nihanju pravimo harmonično nihanje.
V naravi imamo zelo redko primer idealnega harmonični nihanje. Oblika nihaja je največkrat popačen sinus, ki pa ga lahko matematično vedno razstavimo na vsoto harmoničnih nihanj. Zato pravimo harmoničnemu nihanju tudi osnovno nihanje.
Predstavljajmo si nihanje uteži pritrjene na lahko vrvico, kot kaže slika. To je nitno nihalo.
Nitno nihalo.
Nihalo sprva miruje v ravnovesni legi. Zaniha le, če mu dodamo energijo. Ko ga izmaknemo iz ravnovesne lege in mu damo potencialno energijo. Nihalo nato spustimo. Potencialna energija se mu postopno pretvarja v kinetično energijo. Največjo kinetično energijo in s tem največjo hitrost doseže v ravnovesni legi. Energija se mu zatem pretvori nazaj v potencialno energijo. Proces se nato ponovi v obratni smeri.
Če ni energijskih izgub je vsota obeh energij v vseh legah nihala enaka. Imenuje se polna energija nihala.
V naslednjem poglavju bomo videli, da je harmonično nihanje dejansko projekcija kroženja na tisto os pravokotnega koordinatnega sistema, ki predstavlja odmik od ravnovesne lege.
Definicije:
Ravnovesna lega nihala je lega, v katerem bi nevzbujeno nihalo mirovalo.
Amplituda nihanja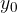 
je maksimalni ali temenski odmik od ravnovesne lege
Nihajni čas je čas, ko se nihalo po nihaju ponovno vrne v začetno lego. Govorimo tudi o periodi nihanja.
Frekvenca nihanja je recipročna vrednost nihajnega časa. Pove, koliko nihajev naredi nihalo na sekundo (ali kolikokrat zaniha v N sekundah)
Harmonično ali sinusno nihanje nihala je primer, ko je trenutni odmik od ravnovesne lege sinusna funkcija časa.
Nitno nihalo, omenjeno v uvodu je le pogojno harmonično nihalo. V gradivu Nihala bomo videli, da niha približno sinusno le, če je amplituda nihanja dovolj majhna glede na dolžino vrvice.
Opazujmo odmik od ravnovesne lege, hitrost in pospešek pri harmoničnem nihanju. Začetek opazovanja je lahko poljuben. Dogovorimo se, da opazujemo nihanje od trenutka, ko gre nihalo skozi ravnovesno lego.
Nihanje idealnega harmoničnega nihala si zamislimo kot projekcijo kroženja na y os,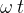 
koordinatnega sistema, kot kaže slika.
Odmik od ravnovesne lege, hitrost in pospešek nihanja. Narisana je ena perioda.
Vzemimo točko na krožnici kroga z radijem 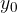. Točka kroži v obratni smeri urinega kazalca in opisuje kot:
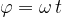
Projekcija točke na krožnici na y os opisuje trenutno vrednost odmika od ravnovesne lege harmoničnega nihala:
Hitrost nihanja je odvod odmika od ravnovesne lege po času. Če še ne obvladamo odvoda, si predstavljamo hitrost kot naklon grafa poti (odmika od ravnovesne lege) po času.
Iz zgornjega grafa vidimo, da je naklon y(t) največji v ravnovesni legi. Funkcija, ki opisuje naklon sinusne funkcije je kosinusna funkcija:
Hitrost je torej največja v ravnovesni legi. Je sorazmerna kotni hitrosti in temenskemu odmiku. Matematično naprednejši lahko to dokažejo s pomočjo odvoda.
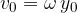
Pospešek nihanja je odvod hitrosti po času. Če še ne obvladamo odvoda, si predstavljamo pospešek kot naklon grafa hitrosti po času. Na grafu hitrosti se vidi, da je naklon največji pri temenskem odmiku od ravnovesne lege.
Brez matematične razlage zapišemo:
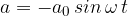
Temenska vrednost pospeška je sorazmerna hitrosti in kotne hitrosti. Matematično naprednejši lahko to pokažejo s pomočjo odvoda - glej naslednje poglavje. Pospešek je največji v legi, ko je hitrost nihanja nič, torej pri največjem odmiku od ravnovesne lege.
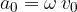
Odmik od ravnovesne lege harmoničnega nihala od trenutka, ko gre skozi ravnovesno lego opisuje enačba:
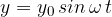
Hitrost nihanja je:
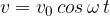
Največja hitrost je v ravnovesni legi (y = 0):
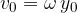
Pospešek nihanja je:
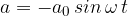
Temenska vrednost pospeška je pri maksimalnem odmiku od ravnovesne lege:
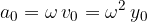
To poglavje je namenjeno učencem, ki so že osvojili poglavje odvodov. Učenci brez znanja odvodov lahko to poglavje brez škode preskočijo.
Znak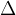 
je velikokrat uporabljen kot srednješolski nadomestek odvoda 
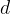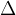. pomeni razliko (npr. časovno razliko), ta razlika pa je lahko poljubno velika. Znak 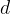, tako kot 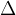, prav tako pomeni razliko, a le neskončno majhno razliko.
Da bomo dobili hitrost kot odvod poti po času najprej zamenjamo znak 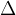v enačbi (2) z d:
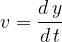
Odmik y je sinusna funkcija časa. Enačbo (1) odvajamo po pravilih za odvajanje. Dobimo:
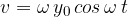
Faktor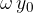 
predstavlja največjo hitrost:
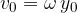
Podobno izračunamo pospešek kot odvod hitrosti po času. V ta namen zamenjamo znak 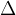v enačbi (3) z d:
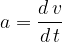
Hitrost v je kosinusna funkcija časa. Enačbo (3) odvajamo po pravilih za odvajanje. Dobimo:
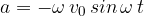
Faktor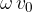 
predstavlja največji pospešek:
