Osebne zbirke


Hiperbola je množica vseh točk v ravnini, za katere je absolutna vrednost razlika razdalj od dveh danih točk 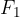 in
in 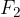 konstanta. Točki
konstanta. Točki 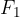 in
in 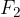 imenujemo gorišči hiperbole.
imenujemo gorišči hiperbole.
Geometrijsko definicijo hiperbole lahko zapišemo kot:
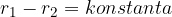
Za enačbo hiperbole kot krivulje drugega reda je značilno, da sta kvadratna člena različno predznačena:
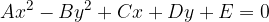
Enačbo hiperbole bomo lažje razumeli s pomočjo skice, zato najprej narišimo skico tipične hiperbole:
V hiperboli (glej skico) nastopajo naslednji značilni elementi:
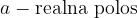
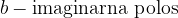
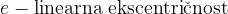
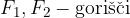
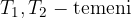
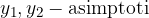
Gorišči hiperbole sta določeni z linearno ekscentričnostjo e (razberemo s skice):
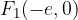
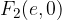
povezanost linearne ekscentričnosti hiperbole e z realno polosjo a in imaginarno polosjo b lahko razberemo s skice:
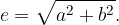
Numerična ekscentričnost hiperbole je:
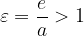
Temeni hiperbole pa sta točki (preberemo s skice):
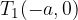
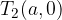
Asimptoti sta dve sekajoči se premici katerim se veji hiperbole približujeta. Enačbi asimptot hiperbole sta:
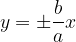
Enačba hiperbole v segmentni obliki:
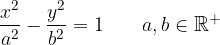
Za lažje razumevanje si narišimo skico hiperbole z realno osjo na ordinatni osi:
Značilni elementi hiperbole so na ordinatni osi:
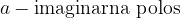
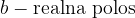
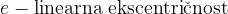
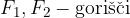
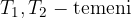
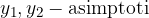
Gorišči hiperbole sta določeni z linearno ekscentričnostjo e (razberemo s skice):
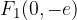
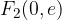
povezanost linearne ekscentričnosti hiperbole e z imaginarno polosjo a in realno polosjo b lahko razberemo s skice:
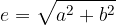
Numerična ekscentričnost hiperbole je:
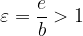
Temeni hiperbole sta točki (razberemo s skice)
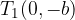
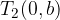
Enačbi asimptot hiperbole sta:
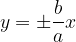
Enačba hiperbole v segmentni obliki:
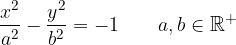
Središče hiperbole je lahko tudi zunaj koordinatnega izhodišča npr. v točki 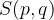 . Narišimo hiperbolo s središčem
. Narišimo hiperbolo s središčem 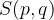 :
:
Gorišči hiperbole sta točki 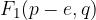 in
in 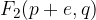 , kjer je e linearna ekscentričnost hiperbole:
, kjer je e linearna ekscentričnost hiperbole:
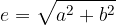
Temeni hiperbole sta točki
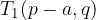
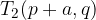
Enačbi asimptot hiperbole sta:
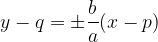
Enačba hiperbole s središčem v točki 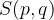 :
:
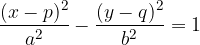
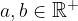
Kadar iščemo presečišče med hiperbolo in premico rešujemo sistem njunih enačb:
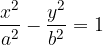
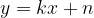
Rešitev poiščemo tako, da y premice vstavimo v enačbo hiperbole. V splošnem poznamo tri rešitve:
Prva rešitev: tangenta
Premica je tangenta, če ima sistem eno dvojno rešitev:
Druga rešitev: sekanta
Če ima sistem dve različni rešitvi ali eno rešitev, ki ni dvojna je premica sekanta.
Tretja rešitev: brez skupnih točk
Če sistem nima realnih rešitev, premica s hiperbolo nima skupnih točk.