Osebne zbirke


Hornerjev algoritem je postopek, ki nam olajša izvajanje določenih operacij na polinomih. Te operacije so:
računanje vrednosti polinoma
deljenje danega polinoma z linearnim polinomom (linearno funkcijo)
iskanje ničel danega polinoma
Reševanje polinomov poteka tabelarično.
Z uporabo Hornerjevega algoritma lahko lažje računamo vrednosti polinomov višjih stopenj brez zamujajočega računanja posameznih členov, ki privedejo do običajno velikih številk.
Najlažje bo, če si uporabo računanja pogledamo kar na konkretnem primeru.
Pri uporabi Hornerjevega algoritma za računanje s polinomi moramo biti pazljivi pri vpisovanju koeficientov v tabelo. V le-to spadajo tudi koeficienti, ki so enaki 0.
Pri računanju s Hornerjevi algoritmom moramo biti pazljivi tudi na negativni predznak posameznih členov polinoma.
Postopek reševanj polinomov s Hornerjevim algoritmom je enostaven a pazljivi moramo biti pri prepisovanju koeficientov v tabelo:
upoštevati moramo koeficiente, ki so enaki 0 in
upoštevati moramo negativne predznake koeficientov.
Spomnimo se pravila za deljenje polinomov: polinom 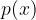 , stopnje m, nam da pri deljenju s polinomom
, stopnje m, nam da pri deljenju s polinomom 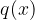 , stopnje n, kvocient
, stopnje n, kvocient 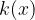 , stopnje (m - n) in ostanek
, stopnje (m - n) in ostanek 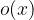 , če velja
, če velja
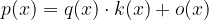
in je stopnja polinoma 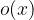 strogo manjša od stopnje delitelja
strogo manjša od stopnje delitelja 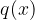 .
.
Ko delimo polinom n-te stopnje s polinomom prve stopnje / linearnim polinomom, lahko slednje pravilo precej poenostavimo.
Deljenje polinoma 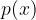 z linearnim polinomom
z linearnim polinomom 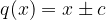 , je enako, kot če bi iskali rešitev polinoma pri
, je enako, kot če bi iskali rešitev polinoma pri 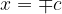 .
.
Dodatno pazljivi moramo biti, ko ima naš linearni polinom prosti člen s pozitivnim predznakom. V tem primeru računamo Hornerjev algoritem z negativnim številom.
Spomnimo se najprej pravila:
Ničla polinoma p(x) je takšna vrednost za neodvisno spremenljivko x, za katero ima polinom vrednost 0.
V primeru Hornerjevega algoritma to pomeni, da ostanek, ki ga dobimo je enak 0. Oziroma, da je dani polinom p(x) deljiv z linearnim polinomom 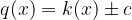 .
.
Polinom p(x), stopnje m, nam da pri deljenju s polinomom q(x), stopnje n, kvocient k(x), stopnje (m - n) in ostanek o(x):
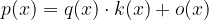
Pri vrednostih x, kjer je ostanek o(x) = 0 ima polinom ničlo.
Potencialne ničle polinoma lahko najdemo med:
delitelji prostega člena 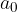
racionalna števila, ki števcu imajo delitelja prostega člena in v imenovalcu delitelja vodilnega člena 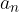
S Hornerjevim algoritmom preverimo primernost potencialnih ničel. Število ničel je enako ali manjše od stopnje polinoma. Če torej imamo polinom 3. stopnje, bo le-ta imel največ 3 ničle.