Osebne zbirke


Racionalna funkcija je funkcija oblike:
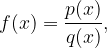
kjer sta 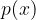 in
in 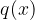 polinoma.
polinoma.
Ko želimo takšno funkcijo integrirati, najprej preverimo stopnji polinomov v števcu in imenovalcu. Glede na stopnji števca in imenovalca v grobem ločimo primera, ko je:
stopnja števca večja ali enaka stopnji imenovalca
stopnja števca manjša od stopnje imenovalca.
Racionalno funkcijo, kjer je števec 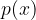 višji ali enak imenovalcu racionalne funkcije, najprej uredimo tako, da števec delimo z imenovalcem. Postopek je popolnoma enak kot pri iskanju asimptote racionalne funkcije:
višji ali enak imenovalcu racionalne funkcije, najprej uredimo tako, da števec delimo z imenovalcem. Postopek je popolnoma enak kot pri iskanju asimptote racionalne funkcije:
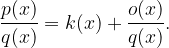
Preurejeno racionalno funkcijo integriramo:
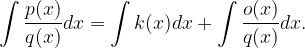
Celi del 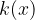 integriramo z uporabo osnovnih pravil integriranja. Za racionalni del
integriramo z uporabo osnovnih pravil integriranja. Za racionalni del 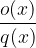 , ki ostane pri deljenju števca z imenovalcem pa velja, da je stopnja števca manjša od imenovalca. Takšno racionalno funkcijo integriramo na enega od načinov, opisanih v nadaljevanju.
, ki ostane pri deljenju števca z imenovalcem pa velja, da je stopnja števca manjša od imenovalca. Takšno racionalno funkcijo integriramo na enega od načinov, opisanih v nadaljevanju.
Poglejmo nekaj različnih primerov takšne racionalne funkcije.
Ker imamo imenovalec, ki ima stopnjo za 1 stopnjo nižjo od števca, v integral uvedemo novo spremenljivko in integriramo osnovni integral.
Integrale, kjer imamo pod integralskim znakom racionalno funkcijo, za katero velja:
stopnja števca je nižja od stopnje imenovalca in
imenovalec je možno razstaviti na linearne faktorje,
rešujemo s pomočjo parcialnih (delnih) ulomkov.
Takšne funkcije običajno ne znamo integrirati neposredno s pomočjo osnovnih integralov. Zato moramo to funkcijo najprej razstaviti na parcialne ulomke, ki pa jih znamo integrirati.
Razcep na parcialne ulomke poteka v več korakih in si ga bomo ogledali na konkretnem primeru.
Poglejmo še primer integracije funkcije 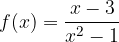 .
.
 števil, števec pa je konstanten
števil, števec pa je konstantenNajprej zapišemo nerazcepen kvadratni polinom v obliki popolnega kvadrata:
Integracije se lotimo tako, da iz imenovalca naredimo popolni kvadrat, uvedemo novo spremenljivko, potem pa vsak integral integriramo po eni izmed uveljavljenih metod.