Osebne zbirke


Interval je v matematiki množica realnih števil, ki ležijo med dvema danima realnima številoma (na realni premici). Ti dve števili imenujemo krajišči. Krajišči sta lahko vključeni v interval ali pa tudi ne.
Interval zapišemo na naslednji način:
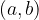
pri čemer je a levo krajišče in b desno krajišče. Oklepaji so odvisni od vrste intervalov. In sicer velja naslednjo pravilo:
Oglati oklepaj označuje, da krajišče sodi k intervalu, npr: 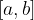 .
.
Okrogli oklepaj označuje, da je interval brez ustreznega krajišča, npr: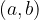 .
.
Naj velja dogovor, da krajišči poimenujemo z a in b, pri čemer je 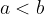 . Ko ponazorimo interval na številski premici, krajišča označujemo s posebnima simboloma. Z odebeljeno piko označujemo, da krajišče sodi k intervalu, s puščico pa, da je interval brez krajišča.
. Ko ponazorimo interval na številski premici, krajišča označujemo s posebnima simboloma. Z odebeljeno piko označujemo, da krajišče sodi k intervalu, s puščico pa, da je interval brez krajišča.
Glede na to, ali krajišči intervala sodita k intervalu ali ne, ločimo več vrst intervalov:
Zaprti interval vključuje poleg vseh števil med a in b tudi obe krajišči; označimo ga z oglatim oklepajem: 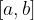
Zaprti interval simbolno zapišemo in definiramo kot:
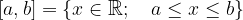
Zaprti interval grafično prikažemo na številski premici kot:
Odprti interval ne vsebuje krajišč - vsebuje samo vsa števila med njima. Označimo ga z okroglim oklepajem: 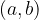
Odprti interval simbolno zapišemo in definiramo kot:
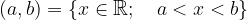
Zaprti interval grafično prikažemo na številski premici kot:
V tem primeru ločimo med naslednjima intervaloma:
Označimo ga na levi strani z okroglim oklepajem in na desni strani z oglatim oklepajem: 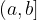
Levo odprti in desno zaprti interval simbolno zapišemo in definiramo kot:
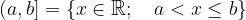
Desno zaprti interval grafično prikažemo na številski premici kot:
Označimo ga na levi strani z oglatim oklepajem in na levi strani z okroglim oklepajem: 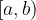
Desno odprti in levo zaprti interval simbolno zapišemo in definiramo kot:
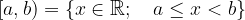
Zaprti interval grafično prikažemo na številski premici kot:
V nadaljevanju si bomo na konkretnem primeru pogledali kako določimo interval:
Množica realnih števil je tudi interval.
Množico realnih števil lahko zapišemo kot interval in sicer:
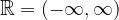
Enako lahko zapišemo še druge večkrat uporabljene podmnožice realnih števil:
Simbolno jo zapišemo kot:

Grafično jo prikažemo kot:
Simbolno jo zapišemo kot:
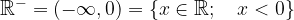
Grafično jo prikažemo kot:
Simbolno jo zapišemo kot:
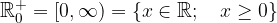
Grafično jo prikažemo kot:
Simbolno jo zapišemo kot:
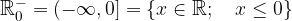
Grafično jo prikažemo kot: