Osebne zbirke


Iskanje ničel polinoma poteka na več različnih načinov:
z razcepom na linearne ali kvadratne polinome,
z deljenjem,
numerične metode.
Potencialni kandidati za ničle so delitelji prostega člena 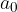 in vodilnega koeficienta
in vodilnega koeficienta 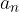 . V primeru, da je vodilni koeficient enak 1, potem so racionalne ničle cela števila.
. V primeru, da je vodilni koeficient enak 1, potem so racionalne ničle cela števila.
V primeru, da je vodilni koeficient 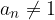 , potem so potencialne ničle racionalna števila
, potem so potencialne ničle racionalna števila 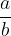 , kjer a je delitelj prostega člena
, kjer a je delitelj prostega člena 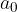 in b je delitelj vodilnega člena
in b je delitelj vodilnega člena 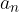 .
.
Polinom n-te stopnje lahko zapišemo tudi v ti. ničelni obliki. Pri določanju posameznih linearni faktorjev si lahko pomagamo z metodo:
z izpostavljanjem skupnega faktorja,
z Vietovim pravilom za kvadratne enačbe,
s formulo za iskanje ničel kvadratne enačbe.
Pri izpostavljanju skupnega faktorja moramo prepoznati le-tega znotraj zapisanega polinoma.
Pri razstavljanju polinomov na linearne faktorje se srečamo tudi s polinomom 2.stopnje. Pri iskanju ničel slednjega lahko uporabimo Vietovo pravilo.
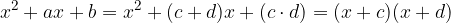
V primeru, ko je vodilni koeficient 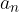 pri kvadratni enačbi različen od 1. Raje uporabimo formulo za iskanje ničel kvadratne enačbe, katere postopek je podrobneje razložen v poglavju Ničelna oblika in ničle kvadratne funkcije.
pri kvadratni enačbi različen od 1. Raje uporabimo formulo za iskanje ničel kvadratne enačbe, katere postopek je podrobneje razložen v poglavju Ničelna oblika in ničle kvadratne funkcije.
Obnovimo. Za polinom oblike:
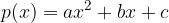
velja
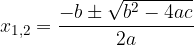
Če je diskriminanta 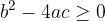 , dobimo realne ničle.
, dobimo realne ničle.
V primeru, da je diskriminanta 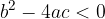 , dobimo kompleksne ničle z imaginarno enoto.
, dobimo kompleksne ničle z imaginarno enoto.
Postopek deljenja polinomov lahko pogledamo v poglavju Deljenje polinomov. Pri iskanju ničel polinomov n-te stopnje lahko preverimo, ali pri deljenju izbranega polinoma z linearni polinomom dobimo ostanek nič. V tem primeru pri danem x imamo ničlo.
Če lahko kvocient polinoma z linearno funkcijo zapišemo kot:
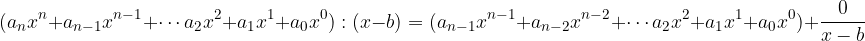
potem je
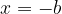
ničla polinoma.
Iskanje ničel s Hornerjevim algoritmom je tabelaričen postopek računanja vrednosti polinoma pri danem x. Računanje poteka izključno z posameznimi koeficienti, s tem se izognemo računanju visokih potenc.
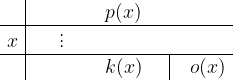
V prvo vrstico zapišemo koeficiente danega polinoma 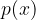 , v drugi vrstici zapišemo potencialno ničlo
, v drugi vrstici zapišemo potencialno ničlo 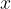 . Po seriji enostavnih računskih operacij dobimo koeficiente polinoma nižje stopnje
. Po seriji enostavnih računskih operacij dobimo koeficiente polinoma nižje stopnje 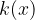 in ostanek
in ostanek 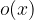 . Če je dana vrednost ničla, potem je ostanek
. Če je dana vrednost ničla, potem je ostanek