Prijava z e-naslovom
Prijava brez gesla
Izjave in izjavne povezave so glavni predmet proučevanja v logiki. Kaj pa pravzaprav je izjava?
Izjava je smiselni povedni stavek. Izjave so lahko:
pravilne in jim dodelimo vrednost p (kot pravilno) ali 1;
nepravilne in jim dodelimo vrednost n (kot nepravilno) ali 0.
Poznamo dve vrsti izjav, in sicer
elementarne ali enostavne izjave
sestavljene izjave.
Elementarne izjave ne moremo razstaviti na bolj enostavne.
Da je izjava sestavljena nam običajno pokažejo vezniki (in, ali) ali pa je kako drugače nakazano v stavku (glej podpoglavje sestavljene izjave).
Sestavljene izjave zgradimo iz enostavnih izjav z uporabo izjavnih povezav. Izjavne povezave so neke vrste operatorji (kot + in - pri seštevanju števil) s katerimi povezujemo izjave.
Da ugotovimo ali je sestavljena izjava pravilna ali ne, moramo najprej ugotoviti vrednosti enostavnih izjav in pripadajočih izjavnih povezav.
Izjavne povezave so lahko:
enočlene ali
dvočlene
Enočlena izjavna povezava je taka povezava, ki jo lahko uporabimo že na eni sami izjavi.
Naj bo dana izjava A. Negacijo izjave A označimo z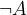 
, zanjo pa velja:
NEGACIJA izjave A je izjava, ki trdi nasprotno kot izjava A.
Negacija negacije izjave je izjava sama: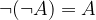 
Če je izjava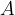 
pravilna, je 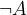nepravilna. Če pa je 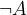pravilna, je 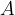nepravilna. To ponazorimo s pravilnostno tabelo:
Dvočlene povezave so povezave, ki povezujejo po dve izjavi. Te so:
konjunkcija
disjunkcija
implikacija
ekvivalenca
Konjunkcija je operacija, ki dve izjavi poveže z zvezo "in hkrati". Če sta dani izjavi A in B, matematično konjunkcijo označimo z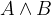 
.
Naj bosta dani dve izjavi: A in B. Velja:
konjunkcija izjav A in B nastane tako, da obe izjavi povežemo z zvezo "in hkrati";
oznako 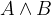beremo:
daljša verzija: "velja izjava A in hkrati velja izjava B"
krajša verzija: "A in hkrati B";
konjunkcija je pravilna samo takrat, kadar sta pravilni tako izjava A kot tudi izjava B. To ponazorimo s pravilnostno tabelo:
konjunkcija je komutativna in asociativna (podobno kot pri seštevanju in množenju naravnih števil):
komutativnost:
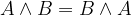
asociativnost:
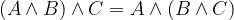
Disjunkcija je operacija, ki dve izjavi poveže z zvezo "ali". Če sta dani izjavi A in B, matematično disjunkcijo označimo z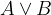 
.
Naj bosta dani dve izjavi: A in B. Velja:
disjunkcija izjav A in B nastane tako, da obe izjavi povežemo z zvezo "ali";
oznako 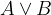beremo:
daljša verzija: "velja izjava A ali izjava B"
krajša verzija: "A ali B";
če sta izjavi A in B nepravilni, je nepravilna tudi njuna disjunkcija, v preostalih primerih je pravilna. To ponazorimo s pravilnostno tabelo:
tudi disjunkcija je komutativna in asociativna:
komutativnost:
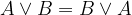
asociativnost:
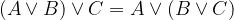
Za konjunkcijo in disjunkcijo pa veljata še dva zakona:
Distributivnostni zakon
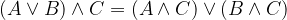
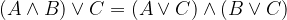
De Morganov zakon
Negacija konjunkcije izjav je disjunkcija negacij posameznih izjav:
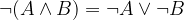
Negacija disjunkcije izjav je konjunkcija negacij posameznih izjav:
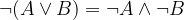
Implikacija je operacija, ki dve izjavi poveže z zvezo "sledi". Če sta dani izjavi A in B, matematično implikacijo označimo z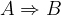 
.
Naj bosta dani dve izjavi: A in B. Velja:
implikacija izjav A in B nastane tako, da obe izjavi povežemo z zvezo "sledi";
oznako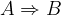 
beremo:
daljša verzija: ''iz izjave A sledi izjava B''
krajša verzija: "iz A sledi B";
drug način branja implikacije: ''če velja izjava A, potem velja izjava B.''
izjava A je pogoj, izjava B pa posledica izjave A. Če je izjava A pravilna in je izjava B nepravilna (pogoj pravilen, posledica pa nepravilna) je nepravilna tudi implikacija, v preostalih primerih je pravilna. To ponazorimo s pravilnostno tabelo:
Ekvivalenca je operacija, ki dve izjavi poveže z zvezo "če in samo če". Če sta dani izjavi A in B, matematično ekvivalenco označimo z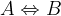 
.
Naj bosta dani dve izjavi: A in B. Velja:
ekvivalenca izjav A in B nastane tako, da obe izjavi povežemo z zvezo "če in samo če";
oznako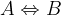 
beremo:
daljša verzija: ''izjava A velja, če in samo če velja izjava B.''
druga verzija: ''izjava A velja natanko tedaj, ko velja izjava B.''
če sta obe izjavi pravilni ali obe nepravilni je ekvivalenca izjav pravilna. Ekvivalenca je nepravilna, če imata izjavi različno vrednost (ena je pravilna druga nepravilna). To ponazorimo s pravilnostno tabelo:
V logiki enakovredni oziroma ekvivalentni izjavi pomenita eno in isto in ju lahko nadomestimo drugo z drugo. Zelo uporabna ekvivalenca pri nalogah z dokazovanjem je:
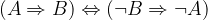
Sestavljeni izjavi, ki je pravilna pri vseh naborih vrednosti osnovnih izjav, pravimo tavtologija.
Izjavi, ki je vedno neresnična ne glede na naravo delnih izjav, rečemo kontradikcija.
Kot pri računanju s števili (kjer ima množenje prednost pred seštevanjem), moramo tudi v izjavnem računu upoštevati vrstni red ''operacij'' oziroma prioriteto izjavnih povezav. Naštete so izjavne povezave od najvišje prioritete (1.) pa do najnižje prioritete (5.):
Negacija
Konjunkcija
Disjunkcija
Implikacija
Ekvivalenca
Če moramo zapored izvesti več enakih izjavnih povezav uporabimo pravilo združevanja od leve proti desni.
