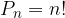Prijava z e-naslovom
Prijava brez gesla
Kombinatoriko lahko primerjamo tudi s preslikavami. Kot že vemo, je preslikava ali funkcija predpis, ki vsakemu elementu iz prve množice priredi natanko določen element iz druge množice. Pri tem poznamo tri vrste preslikav:
injektivna preslikava
surjektivna preslikava
bijektivna preslikava
Poglejmo si, kako lahko kombinatoriko primerjamo z vsako od treh preslikav.
Preslikava je injektivna takrat, ko se preslikata dva različna elementa iz prve množice v dva različna elementa v drugi množici.
Primer injektivne preslikave
Ta primer injektivne preslikave nam pokaže le eno od možnosti, kjer se vsako "dekle" iz prve množice preslika v različen "cvet" v drugi množici. Ta možnost nam predstavlja tudi eno kombinacijo, seveda pa lahko v nadaljevanju izberemo še več različnih kombinacij. Tako vidimo, da lahko vsako preslikavo enačimo z eno od možnih kombinacij.
Kot vidimo, nam variacije brez ponavljanja predstavljajo injektivno preslikavo. Pri danemu r in n, kjer je n število elementov v drugi množici in r število elementov iz prve množice, je število vseh kombinacij
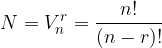
To je natanko enako številu vsek injektivnih preslikav, ko slikamo iz ene množice z r elementi v drugo množico z n elementi (in je r < n).
Preslikava je surjektivna, ko se v vsak element druge množice preslika vsaj en element iz prve množice.
Primer surjektivne preslikave
Ta primer surjektivne preslikave nam pokaže le eno od možnosti, kjer se v vsak "cvet" iz druge množice preslika vsaj ena od "deklet" iz prve množice. Ta možnost nam predstavlja tudi eno kombinacijo, seveda pa lahko v nadaljevanju izberemo še več različnih kombinacij. Tako vidimo, da lahko vsako preslikavo enačimo z eno od možnih kombinacij.
Ne moremo reči, da nam variacije s ponavljanjem predstavljajo surjektivno preslikavo v celoti. Vidimo pa, da nam samo nekatere možnosti izmed danih izbir predstavljajo takšno preslikavo.
Preslikava je bijektivna, če je injektivna in surjektivna hkrati oziroma takrat, ko se vsak element iz prve množice preslika v natanko en element iz druge množice. Število elementov prve množice je enako številu elementov druge množice.
Primer bijektivne preslikave
Ta primer bijektivne preslikave nam pokaže le eno od možnosti, kjer se vsaka od "deklet" iz prve množice preslika v natanko en "cvet" iz druge množice. Ta možnost nam predstavlja tudi eno kombinacijo, seveda pa lahko v nadaljevanju izberemo še več različnih kombinacij. Tako vidimo, da lahko vsako preslikavo enačimo z eno od možnih kombinacij.
Imamo dve enako veliki množici, kjer se vsak element iz prve množice preslika v natanko en elementa iz druge množice. V tem primeru je število bijektivnih preslikav (ali permutacij brez ponavljanja) enako natanko:
