Osebne zbirke


Ko želimo koreniti negativno število, na primer 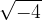 , oziroma poiskati odgovor, katero število množeno samo s seboj da negativen rezultat, na primer
, oziroma poiskati odgovor, katero število množeno samo s seboj da negativen rezultat, na primer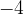 , naletimo na težavo (očitno je, da niti 2 niti - 2 nista pravi odgovor). Odgovor lahko dobimo z uvedbo kompleksnih števil.
, naletimo na težavo (očitno je, da niti 2 niti - 2 nista pravi odgovor). Odgovor lahko dobimo z uvedbo kompleksnih števil.
Kompleksno število je novo število, ki ga doslej še nismo spoznali. V nadaljevanju poglejmo, kako je sestavljeno.
Razširimo doslej največjo množico realnih števil. V ta namen najprej uvedemo novo, imaginarno enoto 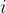 .
.
Imaginarna enota i je definirana kot:
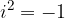
Pogosto se pojavlja napačna definicija imaginarne enote v obliki:
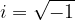
saj je kvadratni koren definiran le za nenegativna števila. Da je gornja oblika napačna, je razvidno iz naslednjega protislovnega primera:
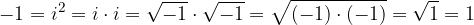
Imaginarna enota i omogoča ovrednotenje negativnih števil pod kvadratnim korenom. Poglejmo si to na konkretnem primeru.
Vsak kvadratni koren iz negativnega števila je torej mogoče napisati v obliki z imaginarno enoto:
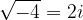
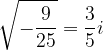
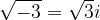
itd....
Vsa dobljena števila imajo obliko:
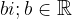
Imenujemo jih imaginarna števila.
Kompleksno število je sestavljeno iz dveh delov:
realnega in
imaginarnega.
V splošni obliki ga zapišemo ga kot vsoto:
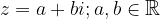
kjer je:
Ko določamo imaginarno komponento kompleksnega števila popazimo, da jo pravilno določimo:
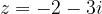 je imaginarna komponenta
je imaginarna komponenta 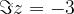 in ne
in ne 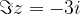
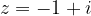 je imaginarna komponenta
je imaginarna komponenta 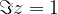 in ne
in ne 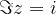 .
.
Množica kompleksnih števil 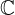 torej predstavlja razširitev realnih števil
torej predstavlja razširitev realnih števil 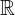 , v kateri lahko korenimo tudi negativna števila:
, v kateri lahko korenimo tudi negativna števila:
Za realno komponento kompleksnega števila 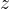 bomo uporabljali naslednje zapise:
bomo uporabljali naslednje zapise:
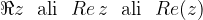
Za imaginarno komponento kompleksnega števila 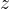 bomo uporabljali naslednje zapise:
bomo uporabljali naslednje zapise:
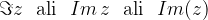
Vsi zapisi so vsebinsko enaki.
Realna števila smo ponazorili na številski osi. Ta števila zasedejo celotno os. Ko želimo uvesti še imaginarna števila, ki imajo glede na realna števila tudi nove lastnosti, jih moramo nanašati na novo, imaginarno os.
Kompleksna števila geometrijsko ponazorimo v kompleksni (Gaussovi) ravnini.
Osnova kompleksne ravnine je pravokotni koordinatni sistem:
Na abscisni osi ponazorimo realna števila. Imenujemo jo realna os in jo označujemo z Re.
Na ordinatni osi ponazorimo imaginarna števila. Imenujemo jo imaginarna os in jo označujemo z Im.
Kompleksno število z, ki je par realnega in imaginarnega števila, ponazorimo v kompleksni ravnini s točko. Njena abscisa je po vrednosti enaka realni komponenti, ordinata pa imaginarni komponenti kompleksnega števila. Velja tudi obratno: vsaki točki kompleksne ravnine ustreza natanko eno kompleksno število.
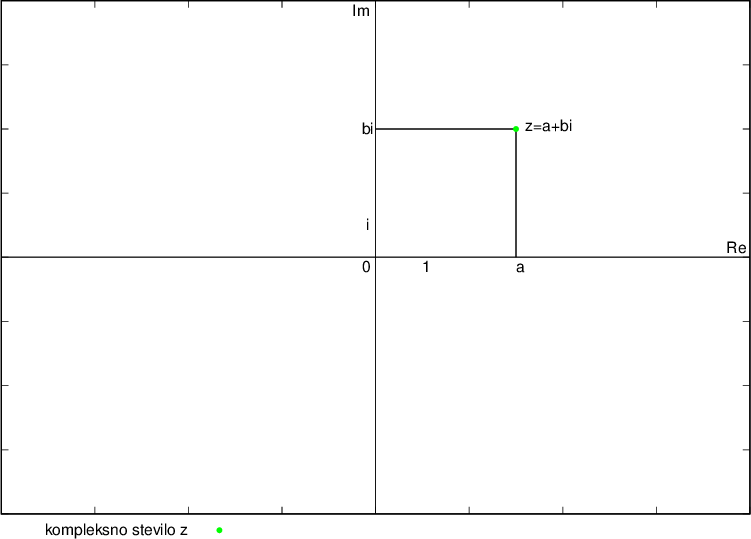
Poglejmo nekaj množic točk 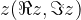 v kompleksni ravnini, pri katerih koordinati
v kompleksni ravnini, pri katerih koordinati 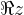 in
in 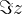 ustrezata kakšnim določenim pogojem:
ustrezata kakšnim določenim pogojem:
Če je v pogoju znak  ali
ali 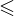 je rešitev področje kompleksne ravnine vključno z njegovim robom (narisan s polno črto).
je rešitev področje kompleksne ravnine vključno z njegovim robom (narisan s polno črto).
Če je v pogoju znak  ali
ali  je rešitev področje kompleksne ravnine brez njegovega roba (narisan s črtkano črto).
je rešitev področje kompleksne ravnine brez njegovega roba (narisan s črtkano črto).
Števila, katerih realni del je 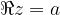 , ležijo na premici, ki je vzporedna imaginarni osi in gre skozi kompleksno število
, ležijo na premici, ki je vzporedna imaginarni osi in gre skozi kompleksno število 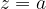 , se pravi točko
, se pravi točko 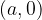 :
:
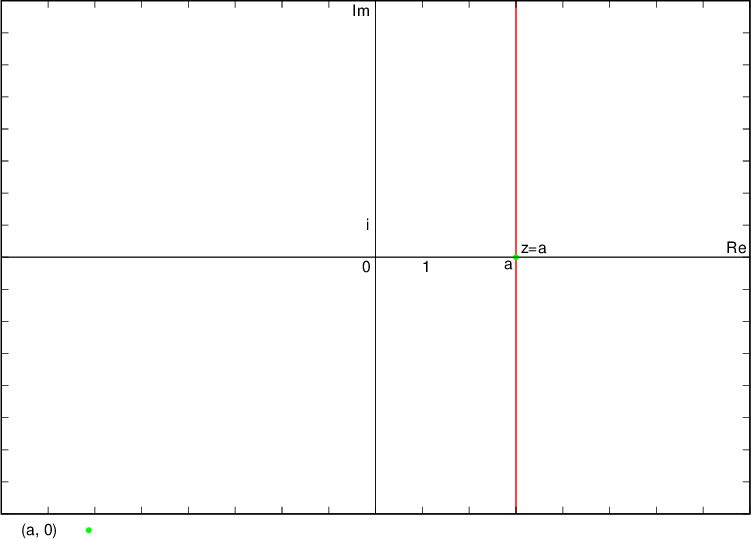
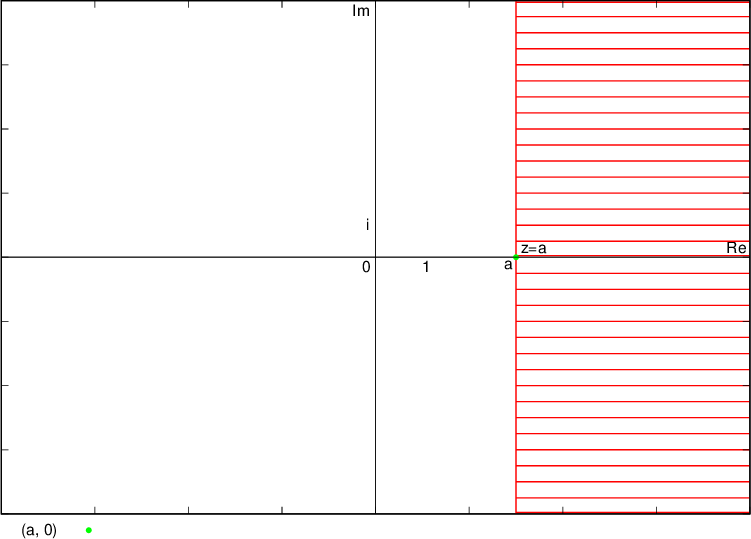
Števila, katerih realni del je  , ležijo na premici in desno od premice (zato premica narisana s polno črto), ki je vzporedna imaginarni osi in gre skozi kompleksno število
, ležijo na premici in desno od premice (zato premica narisana s polno črto), ki je vzporedna imaginarni osi in gre skozi kompleksno število 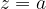 , se pravi točko
, se pravi točko 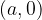 :
:
Števila, katerih realni del je 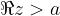 , ležijo desno od premice (zato premica narisana s črtkano črto), ki je vzporedna imaginarni osi in gre skozi kompleksno število
, ležijo desno od premice (zato premica narisana s črtkano črto), ki je vzporedna imaginarni osi in gre skozi kompleksno število 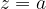 , se pravi točko
, se pravi točko 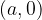 :
:
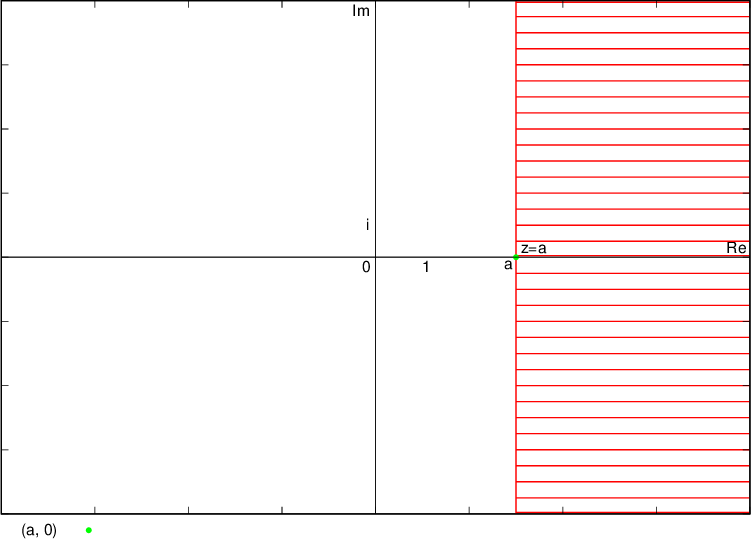
Števila, katerih realni del je 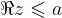 , ležijo na premici in levo od premice (zato premica narisana s polno črto), ki je vzporedna imaginarni osi in gre skozi kompleksno število
, ležijo na premici in levo od premice (zato premica narisana s polno črto), ki je vzporedna imaginarni osi in gre skozi kompleksno število 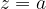 , se pravi točko
, se pravi točko 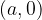 :
:

Števila, katerih realni del je 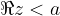 , ležijo levo od premice (zato premica narisana s črtkano črto), ki je vzporedna imaginarni osi in gre skozi kompleksno število
, ležijo levo od premice (zato premica narisana s črtkano črto), ki je vzporedna imaginarni osi in gre skozi kompleksno število 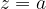 , se pravi točko
, se pravi točko 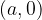 :
:

Števila, katerih imaginarni del je 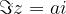 , ležijo na premici, ki je vzporedna realni osi in gre skozi kompleksno število
, ležijo na premici, ki je vzporedna realni osi in gre skozi kompleksno število 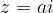 , se pravi točko
, se pravi točko 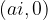 :
:
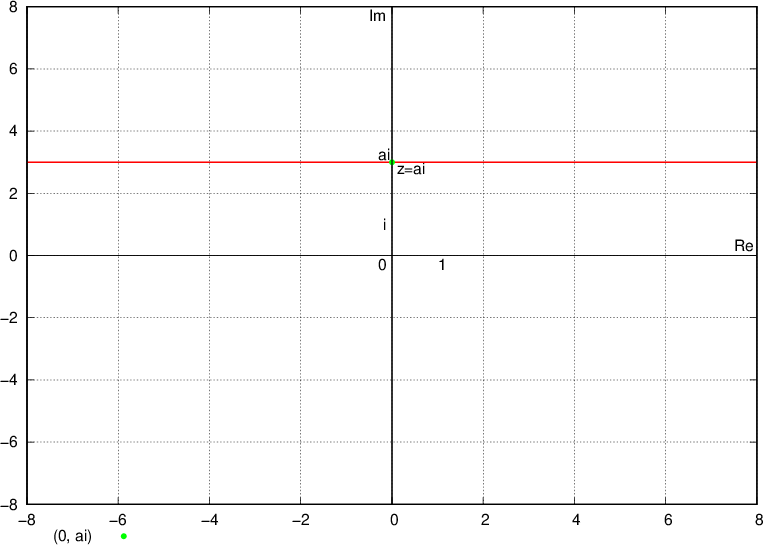
Števila, katerih imaginarni del je 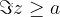 , ležijo na premici in nad premico (zato premica narisana s polno črto), ki je vzporedna realni osi in gre skozi kompleksno število
, ležijo na premici in nad premico (zato premica narisana s polno črto), ki je vzporedna realni osi in gre skozi kompleksno število 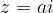 , se pravi točko
, se pravi točko 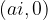 :
:
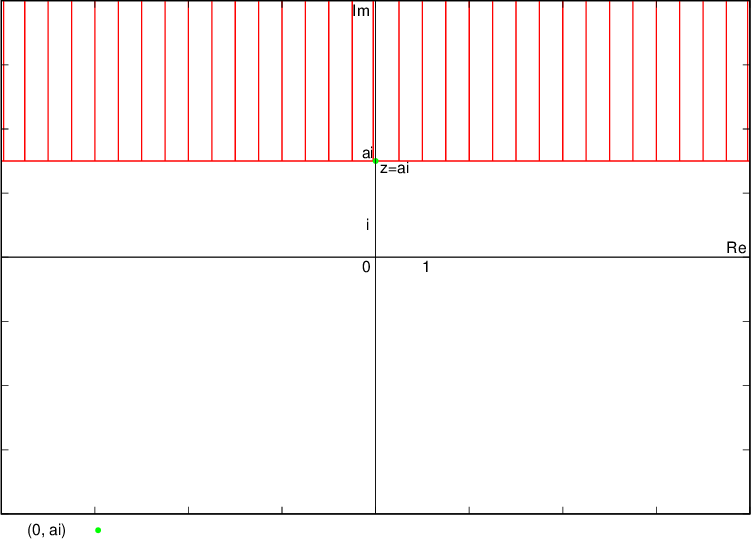
Števila, katerih imaginarni del je 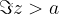 , ležijo nad premico (zato premica narisana s polno črto), ki je vzporedna realni osi in gre skozi kompleksno število
, ležijo nad premico (zato premica narisana s polno črto), ki je vzporedna realni osi in gre skozi kompleksno število 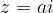 , se pravi točko
, se pravi točko 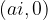 :
:
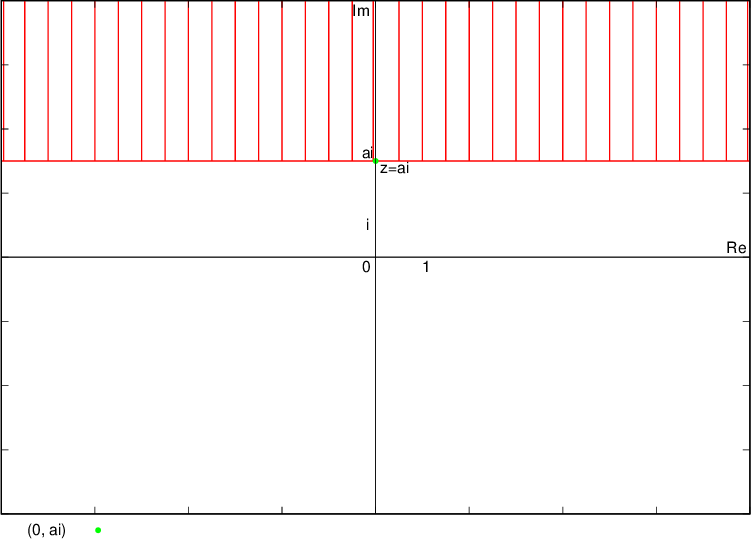
Števila, katerih imaginarni del je 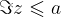 , ležijo na premici in pod premico (zato premica narisana s polno črto), ki je vzporedna realni osi in gre skozi kompleksno število
, ležijo na premici in pod premico (zato premica narisana s polno črto), ki je vzporedna realni osi in gre skozi kompleksno število 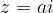 , se pravi točko
, se pravi točko 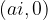 :
:
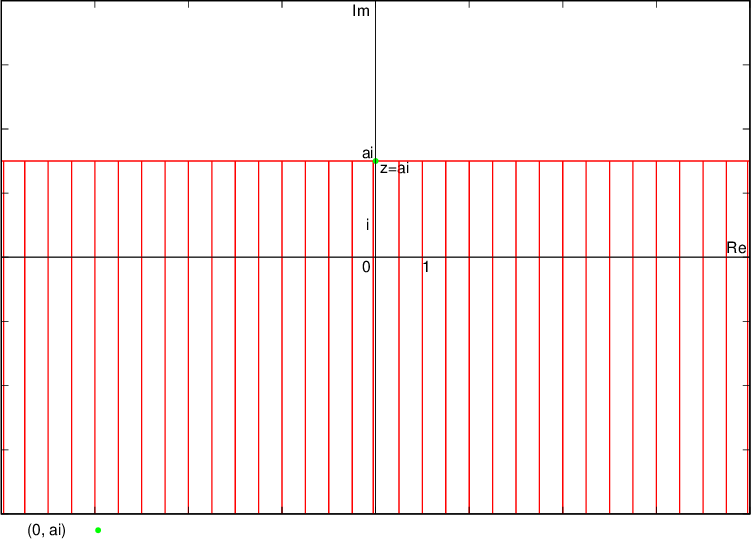
Števila, katerih imaginarni del je 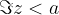 , ležijo pod premico (zato premica narisana s črtkano črto), ki je vzporedna realni osi in gre skozi kompleksno število
, ležijo pod premico (zato premica narisana s črtkano črto), ki je vzporedna realni osi in gre skozi kompleksno število 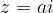 , se pravi točko
, se pravi točko 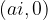 :
:
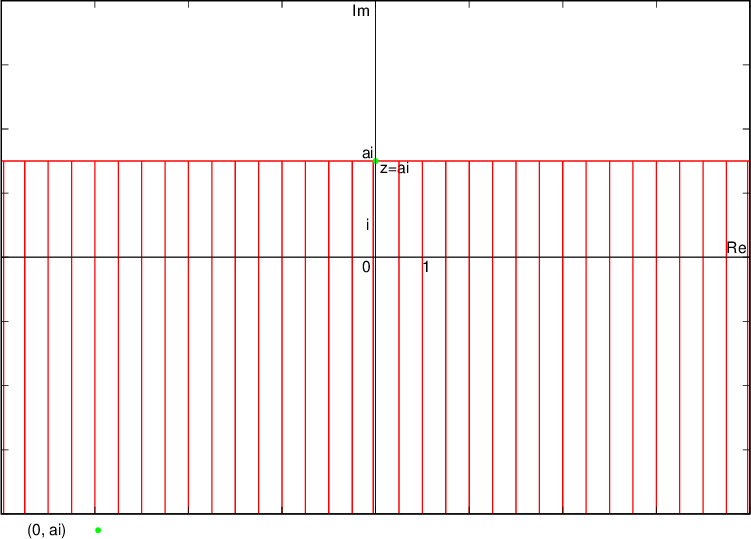
Števila, katerih realni del ustreza pogoju 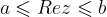 , ležijo na premicah (zato sta premici narisani s polnima črtama) in ravninskem pasu med premicama, ki sta vzporedni imaginarni osi in gresta skozi kompleksni števili
, ležijo na premicah (zato sta premici narisani s polnima črtama) in ravninskem pasu med premicama, ki sta vzporedni imaginarni osi in gresta skozi kompleksni števili 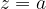 in
in 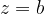 , se pravi točki
, se pravi točki 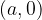 in
in 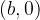 :
:

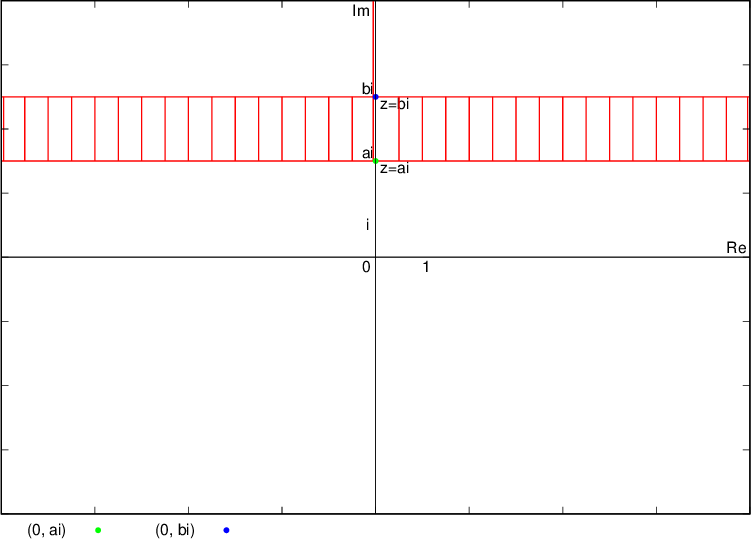
Števila, katerih imaginarni del ustreza pogoju 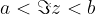 , ležijo na ravninskem pasu med premicama (zato sta premici narisani s črtkanima črtama), ki sta vzporedni realni osi in gresta skozi kompleksni števili
, ležijo na ravninskem pasu med premicama (zato sta premici narisani s črtkanima črtama), ki sta vzporedni realni osi in gresta skozi kompleksni števili 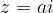 in
in 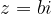 , se pravi točki
, se pravi točki 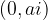 in
in 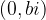 :
:
Števila, ki ustrezajo ustrezajo pogoju 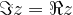 , se pravi, da je njihova imaginarna komponenta enaka realni komponenti, ležijo na simetrali lihih kvadrantov:
, se pravi, da je njihova imaginarna komponenta enaka realni komponenti, ležijo na simetrali lihih kvadrantov:
Če namreč označimo realno komponento kot x, imaginarno pa kot y, lahko zgornji pogoj zapišemo kot y = x. To pa je enačba simetrale lihih kvadrantov.
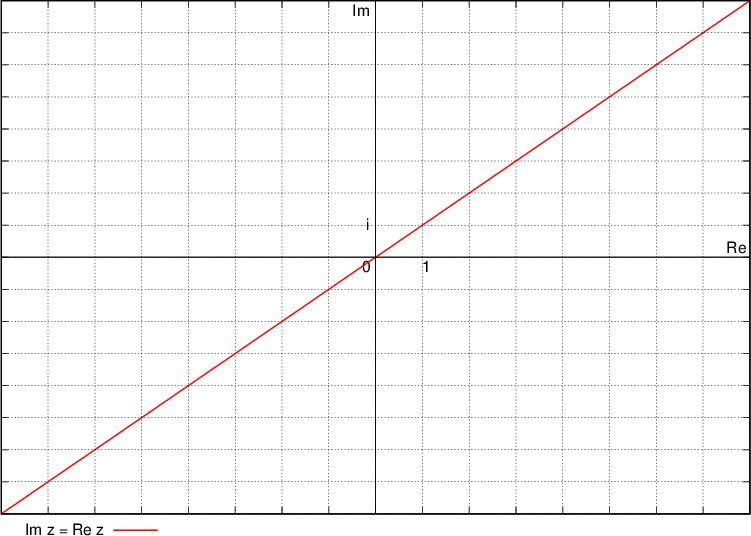
Števila, ki ustrezajo ustrezajo pogoju 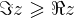 , se pravi, da je njihova imaginarna komponenta večja od realne komponente, ležijo na simetrali (zato je simetrala narisana s polno črto) in nad simetralo lihih kvadrantov:
, se pravi, da je njihova imaginarna komponenta večja od realne komponente, ležijo na simetrali (zato je simetrala narisana s polno črto) in nad simetralo lihih kvadrantov:
