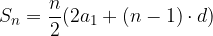Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Končna aritmetična vrsta je vsota prvih n členov aritmetičnega zaporedja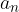 
, kjer je 
:
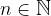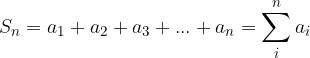
To pomeni, da vsoto končne aritmetične vrsto dobimo tako, da med seboj seštejemo končno število prvih členov aritmetičnega zaporedja. Označimo jo z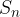 
.
Imamo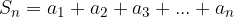 
in želimo izračunati priročnejši obrazec za 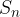. To storimo tako, da končno aritmetično vrsto 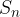namesto
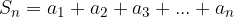
zapišemo kot:
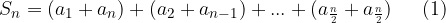
Ker gre za aritmetično zaporedje, vemo, da velja: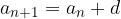 
. Poglejmo, kako lahko preoblikujemo oklepaje enačbe (1):
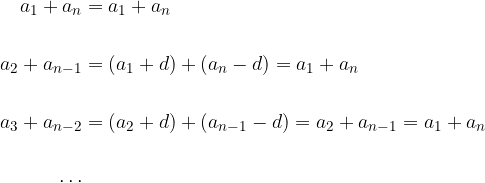
Očitno so vsi oklepaji enačbe (1) enaki 
(dokažemo lahko s popolno indukcijo). Ker imamo takih členov ravno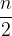 
je obrazec za vsoto končne aritmetične vrste:
Obrazec za vsoto končne aritmetične vrste (za vsoto prvih n členov aritmetičnega zaporedja), kjer 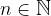je , je:
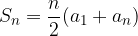
Z upoštevanjem obrazca za splošni člen aritmetičnega zaporedja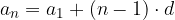 
je obrazec za vsoto prvih n členov tudi:
