Prijava z e-naslovom
Prijava brez gesla
Medsebojno lego števil lahko grafično prikažemo na premici, ki jo imenujemo realna os ali številska os.
Če dve številski osi postavimo pravokotno eno na drugo, dobimo koordinatni sistem, v katerem lahko prikažemo katero koli točko v ravnini.
Realna os je ravna črta, na katero v zaporedju od leve proti desni zapišemo realna števila (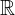
). Imenujemo jo tudi številska os.
Središče osi predstavlja število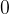 
. Na desno stran od ničle označimo pozitivna števila, na levo stran pa negativna števila.
Na številski osi običajno označimo cela števila, ker je tako os preglednejša in lažja za uporabo.
Določiti je potrebno tudi merilo, ki zagotavlja, da so števila na realni osi enakomerno razporejena.
Merilo izberemo tako, da je koordinata točke usklajena z merilom. To pomeni:
če so vrednosti koordinate majhna števila, potem na merilu izberemo enoto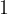 
,
če so vrednosti koordinate večja števila, potem na merilu zapišemo večja števila, na primer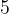 
, 
, 
, 
, 
, 
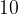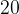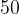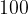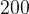..., vedno pa moramo označiti tudi vrednost ene enote.
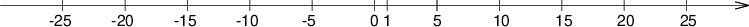
Vsakemu številu pripada ena točka na številski osi in vsaki točki na realni osi pripada točno eno število. To število imenujemo koordinata točke.
Kljub temu, da oznake na številski osi predstavljajo cela števila, je koordinata točke lahko katero koli realno število.
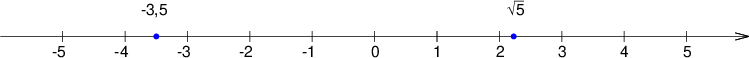
Na vsaki številski osi moramo označiti:
os s puščico proti neskončnosti,
izhodišče 0,
enoto 1.
Na številski osi poleg posameznih točk lahko upodobimo tudi množico točk.
Množico točk predstavljajo vse točke, ki izpolnjujejo določene pogoje. Te pogoje zapišemo s simboli za neenakosti:
... strogo manjše
... manjše ali enako
... strogo večje
... večje ali enako
Na številski osi množico točk, ki izpolnjujejo en pogoj, označimo s poltrakom.
Pri tem velja:
Če je pogoj strog, krajišče intervala ne spada v množico točk in na njegovem mestu narišemo puščico.
Če pogoj ni strog, krajišče intervala spada v množico točk in na njegovem mestu narišemo piko.
Množico točk, ki izpolnjujejo dva pogoja, označimo z daljico.
Pri tem velja:
Če je posamezen pogoj strog, ustrezno krajišče daljice ne spada v množico točk in na njegovem mestu narišemo puščico.
Če posamezen pogoj ni strog, ustrezno krajišče daljice spada v množico točk in na njegovem mestu narišemo piko.
Točko na številski osi označimo s piko ali križcem.
Omejeno množico točk označimo z daljico. Če želimo označiti, da je končna točka daljice zajeta zraven v našem pogoju, potem na tem koncu daljice naredimo piko. Če želimo označiti, da končna točka daljice ni zajeta v našem pogoju, potem na tem koncu daljice naredimo puščico in to pomeni, da smo označili vse točke na številski osi, razen tiste končne, kjer je puščica.
Ko je pogoj v eno smer neomejen, potem bomo množico točk označili s poltrakom. Na neomejenem koncu potegnemo črto do konca številske osi.
Koordinatni sistem v ravnini predstavljata dve premici ali osi, ki se sekata pod pravim kotom. To sta koordinatni osi pravokotnega koordinatnega sistema ter:
vodoravno os imenujemo abscisna os in jo označimo z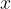 
.
navpično os pa imenujemo ordinatna os in jo označimo z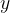 
.
Presečišče koordinatnih osi je točka, ki ji rečemo izhodišče koordinatnega sistema. Označimo jo z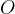 
.
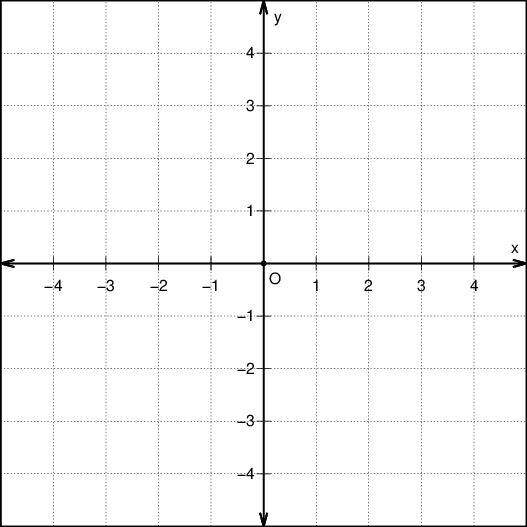
Vsaka točka v koordinatnem sistemu je določena z dvema številoma, ki ju imenujemo koordinati.
prvo koordinato imenujemo abscisa,
drugo koordinato pa imenujemo ordinata.
Koordinate točk vedno zapišemo v obliki urejenega para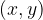 
.
Pravokotni koordinatni sistem je ogrodje, v katerem lahko označimo poljubno točko v ravnini in množice točk. V njem lahko rišemo daljice in geometrijske like ter računamo razdalje in ploščine.
V koordinatnem sistemu predstavimo tudi odvisnost dveh količin, s čimer dobimo graf, ki je običajno lomljena črta ali pa krivulja v koordinatnem sistemu.
Točke v koordinatni sistem narišemo na naslednji način:
Najprej določimo merila osi,
nato poiščemo vrednost abscise 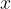na vodoravni osi,
nato poiščemo vrednost ordinate 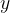na navpični osi,
točko označimo na presečišču teh dveh vrednosti.
Pri risanju ali branju točk pazimo na izbiro ustreznega merila obeh osi, saj s tem zagotovimo, da so točke dobro razporejene in jih lahko natančno odčitamo.
Merilo na oseh je dobro izbrati tako, da so koordinate točk usklajene z merilom. To pomeni:
če so vrednosti 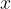in 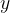majhna števila, potem na merilu izberemo enoto ,
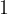če so vrednosti 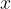in 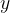večja števila, potem na merilu zapišemo večja števila, na primer 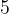, , 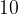, , 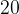, 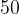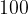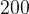... vedno pa moramo označiti tudi vrednost ene enote.
Če imamo v koordinatnem sistemu že označeno točko, potem njene koordinate odčitamo na naslednji način:
Najprej odčitamo vrednost, ki ustreza točki na osi ,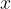
nato odčitamo vrednost, ki ustreza točki na osi .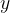
nazadnje koordinati točke zapišemo kot urejeni par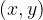 
.
Ko opazujemo odvisnost med količinami, to pogosto prikažemo z:
enačbo,
tabelo vrednosti ali
grafom.
Odvisnosti količin lahko zapišemo matematično, v obliki enačbe ali formule.
Vsaka enačba vsebuje odvisno in neodvisno spremenljivko, dodatno pa so v njej lahko tudi številske vrednosti. Številske vrednosti v enačbah se ne spreminjajo, zato jih imenujemo konstante.
S pomočjo enačbe lahko izračunamo vrednost odvisne spremenljivke za poljubno vrednost neodvisne spremenljivke.
Če vrednost odvisne spremenljivke izračunamo za več vrednosti neodvisne spremenljivke, jih lahko uredimo v obliki tabele:
v prvem stolpcu tabele navedemo vrednosti neodvisne spremenljivke ,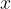
v drugem pa vrednosti odvisne spremenljivke .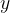
Tabelo uredimo tako, da sta vrednost 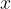in njej pripadajoča vrednost 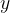ena poleg druge.
Če neodvisne spremenljivke in njim pripadajoče vrednosti odvisnih spremenljivk zapišemo kot urejene pare (točke) in jih prikažemo v koordinatnem sistemu, dobimo graf. Graf je skupek točk v koordinatnem sistemu in prikazuje, kako se vrednosti ene spremenljivke spreminjajo v odvisnosti od druge.
Pri branju grafov se srečamo z dvema vrstama količin:
Neodvisna spremenljivka predstavlja količino, ki jo določimo sami oziroma se spreminja neodvisno od druge količine. Na grafu je običajno prikazana na vodoravni abscisni osi (osi ).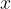
Odvisna spremenljivka predstavlja količino, katere vrednost je odvisna od vrednosti neodvisne spremenljivke. Na grafu je običajno prikazana na navpični ordinatni osi (osi ).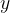
Iz grafa lahko odčitamo vrednost odvisne spremenljivke 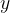pri določeni vrednosti neodvisne spremenljivke .
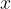Iz grafa lahko razberemo tudi spreminjanje odvisne količine 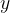glede na neodvisno količino 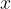. Če se količina povečuje, se graf od leve proti desni dviga, ob zmanjševanju količine pa spušča.
Graf prikaže tudi to, ali se odvisna količina spreminja hitro ali počasi. V območju hitre spremembe je graf strmejši, v območju počasne spremembe pa položnejši.
