Osebne zbirke


Korenjenje je matematična operacija, ki deluje obratno kot potenciranje. Korenjenje zapišemo na naslednji način
Število n je običajno naravno število in ga imenujemo tudi stopnja korena.
Korene poimenujemo glede na njihov korenski eksponent. Torej, če ima koren eksponent:
dva, ga imenujemo kvadratni koren,
tri, ga imenujemo kubični koren,
... ,
n, ga imenujemo n-ti koren.
V nadaljevanju si bomo podrobneje pogledali kvadratni koren in kubični koren ter podali trditve o poljubnem n-tem korenu.
Poiskati kvadratni koren danega števila a 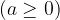 pomeni poiskati tako nenegativno število x, da je
pomeni poiskati tako nenegativno število x, da je 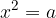 .
.
Za kvadratni koren velja naslednje:
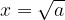
če in samo če je
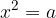
Kvadratni koren ima korenski eksponent število 2, ki ga pri pisanju ponavadi kar izpustimo:
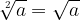
Za kvadratne korene velja še naslednje:
Enačba 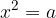 ima za pozitivno število a naslednji rešitvi:
ima za pozitivno število a naslednji rešitvi:
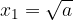
in
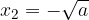
Poglejmo si tri primere računanja kvadratnih korenov:
Poiskati kubični koren danega števila a pomeni, poiskati tako število x, da je 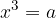 .
.
Za kubični koren velja naslednje:
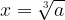
če in samo če je
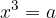
Pri kubičnem korenu je korenjenec lahko negativen, saj je kub negativnega števila negativen. Tako je kubični koren negativnega števila negativen, kubični koren pozitivnega korena pa pozitiven.
Poglejmo si tri primere računanja kubičnih korenov:
Tudi v tem primeru je n-ti koren dobil ime po tem, ker ima za eksponent "n".
V splošnem velja, da za vse korene s sodim korenskim eksponentom mora biti korenjenec pozitiven in za vse korene z lihim korenskim eksponentom je korenjenec lahko pozitiven ali negativen.
Če je n (korenski eksponent) sodo naravno število in 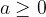 , velja, da je
, velja, da je
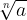
tisto nenegativno realno število, za katerega je :
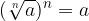
Če je n (korenski eksponent) liho naravno število in a poljubno realno število, velja, da je
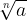
tisto realno število, za katerega je :
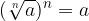
Za lihe korenske eksponente n je:
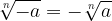
Za vsa pravila v nadaljevanju velja, da morata biti pri sodih korenskih eksponentih 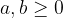
Za ustrezna števila pri računanju s koreni veljajo naslednja pravila:
Če n-ti koren od a potenciramo s potenco n, dobimo za rezultat samo število a (koren in potenca "se pokrajšata)":
Krajšanje potenc (potenciran celoten koren):
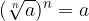
Če ima korenjenec a enako potenco kot je korenski eksponent, dobimo za rezultat samo število a:
Krajšanje potenc (potenciran korenjenec), če je n liho število:
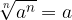
Če pa je n sodo število, pa velja:
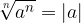
Koren produkta ustreznih števil a in b je enak produktu korena iz a in korena iz b:
Pravilo produkta:
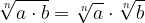
Koren kvocienta ustreznih števil a in b je enak kvocientu korena iz a in korena iz b:
Pravilo kvocienta:
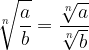
Če je največji skupni deljitelj od stopnje korenjenca in korenskega eksponenta enak r, lahko stopnjo korenjenca in korenski eksponent zdelimo s številom r:
Krajšanje eksponentov:
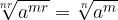
Če imamo korene korenov, jih lahko združimo v en sam koren:
Pravilo o vgnezdenih korenih:
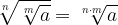
Pozorni moramo biti še na:
Koren vsote ni enak vsoti korenov
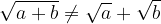
O tem se lahko prepričamo že pri a=b=1, saj je na levi strani rezultat 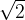 na desni pa
na desni pa 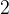 .
.
Delno korenjenje uporabljamo, kadar želimo koreniti števila, ki niso popolni kvadrati, jih pa lahko zapišemo kot produkt popolnega kvadrata in še enega števila. To najlažje storimo po naslednje postopku:
korenjeno število zapišemo v obliki produkta dveh ali več faktorjev; pri tem mora biti vsaj eno število popoln kvadrat
faktorje zapišemo pod svojim korenom
korenimo popolne kvadrate