Osebne zbirke


Kosinusni izrek in sinusni izrek sta izreka, ki veljata v vsakem (poljubnem) trikotniku.
Z njima na podlagi poznanih kotov in/ali stranic ugotavljamo neznane kote in/ali stranice. Omenjeni postopek imenujemo razreševanje trikotnika.
Kosinusni izrek nam služi, da ob podanih:
dveh stranicah in
kotu med njima
izračunamo tretjo stranico.
Kosinusni izrek zapišemo z naslednjimi enačbami:
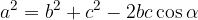
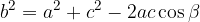
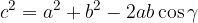
Z ustreznim obračanjem zapisanih enačb pa lahko ob podanih vseh treh stranicah izračunamo kateri koli notranji kot v trikotniku.
S sinusnim izrekom lahko ob podanih:
dveh stranicah in
kotu nasproti ene izmed njih
izračunamo kot nasproti drugi stranici.
Sinusni izrek se glasi:
V trikotniku velja, da je razmerje med sinusom katerega koli kota in dolžino njemu nasproti ležeče stranice konstantno in enako premeru 2R trikotniku očrtanega kroga:
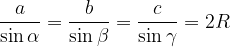
Vedno izberemo tisto enakost, s katero si lahko pomagamo v konkretni nalogi. Če imamo na primer podani stranici a in c ter kot 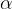 , iščemo pa kot
, iščemo pa kot 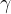 , potem bomo uporabili enačbo:
, potem bomo uporabili enačbo:
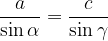
Ob podanih:
dveh kotih in
stranici nasproti enemu izmed njih
lahko izračunamo stranico nasproti drugemu kotu.
Ob podanem radiju trikotniku očrtanega kroga pa lahko:
za kateri koli podani kot izračunamo dolžino nasprotno ležeče stranice ali pa
za katero koli podano stranico izračunamo velikost nasproti ležečega kota.