Osebne zbirke


Za vsa naravna števila 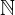 lahko brez konkretnega deljenja povemo, ali so deljiva s števili 2, 3, 4, 5, 6, 7, 8, 9, 10 in 11. To storimo s pomočjo kriterijev deljivosti.
lahko brez konkretnega deljenja povemo, ali so deljiva s števili 2, 3, 4, 5, 6, 7, 8, 9, 10 in 11. To storimo s pomočjo kriterijev deljivosti.
Število 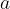 je deljivo z 2, ko je zadnja števka deljiva z 2 oz. ko je zadnja števka sodo število: 0, 2, 4, 6, 8.
je deljivo z 2, ko je zadnja števka deljiva z 2 oz. ko je zadnja števka sodo število: 0, 2, 4, 6, 8.
Splošno: vsa soda števila so deljiva z 2.
Število 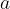 je deljivo s 3, če je vsota števk števila
je deljivo s 3, če je vsota števk števila 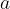 deljiva s 3, tj. vsota števk je večkratnik števila 3.
deljiva s 3, tj. vsota števk je večkratnik števila 3.
Število 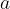 je deljivo s 4, kadar je število, ki ga tvorita zadnji dve števki, tj. desetice in enice, deljivo s 4 ali enaki 0.
je deljivo s 4, kadar je število, ki ga tvorita zadnji dve števki, tj. desetice in enice, deljivo s 4 ali enaki 0.
Število 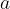 je deljivo s 5, kadar je zadnja števka enaka 0 ali 5.
je deljivo s 5, kadar je zadnja števka enaka 0 ali 5.
Število 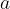 je deljivo s 6, kadar je deljivo z 2 in 3 hkrati.
je deljivo s 6, kadar je deljivo z 2 in 3 hkrati.
Število 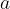 je deljivo s 7, če:
je deljivo s 7, če:
enice števila 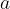 pomnožene z 2
pomnožene z 2
odštejemo od
števila, ki ga dobimo, če številu 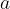 odvzamemo enice
odvzamemo enice
ter je dobljen rezultat enak 0 ali deljiv s 7.
Pri večjih številih je lahko postopek zelo dolgotrajen. V kolikor namreč ne vemo ali je razlika deljiva s 7 oziroma je večkratnik števila 7, isti postopek ponovimo še na rezultatu.
Število 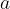 je deljivo z 8, kadar je število, ki ga tvorijo zadnje tri števke števila
je deljivo z 8, kadar je število, ki ga tvorijo zadnje tri števke števila 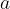 , deljivo z 8.
, deljivo z 8.
Število 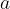 je deljivo z 9, kadar je vsota števk števila
je deljivo z 9, kadar je vsota števk števila 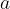 deljiva z 9 oziroma je večkratnik števila 9.
deljiva z 9 oziroma je večkratnik števila 9.
Število 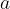 je deljivo z 10, kadar je zadnja števka enaka 0.
je deljivo z 10, kadar je zadnja števka enaka 0.
Naj bo število 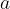 zapisano z nizom števk na naslednji način:
zapisano z nizom števk na naslednji način:
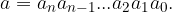
Število 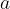 je deljivo z 11, če je alternirajoča vsota
je deljivo z 11, če je alternirajoča vsota
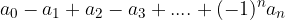
enaka 0 ali deljiva z 11.
Alternirajoča vsota je vsota števil, kjer ima vsako naslednje število v vsoti ravno nasproten predznak od prejšnjega števila.
Število 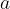 je deljivo z 11, kadar je alternirajoča vsota števk iz desne proti levi enaka 0 ali deljiva z 11.
je deljivo z 11, kadar je alternirajoča vsota števk iz desne proti levi enaka 0 ali deljiva z 11.