Prijava z e-naslovom
Prijava brez gesla
Veliko naravnih pojavov se v določenih časovnih presledkih ponavlja. Poglejmo si nekaj takih, ponavljajočih pojavov.
Opazujmo kolo v zabaviščnem parku.
Kolo v zabaviščnem parku se vrti, kabine pa krožijo okoli osi vrtenja kolesa
Celotno kolo skupaj s kabinami se vrti okoli osi. Za kabine na obodu kolesa pa pravimo, da krožijo po krožnici. Ta krožnica ima polmer enak razdalji med kabinami in osjo vrtenja na sredini kolesa.
Opisani pojavi predstavljajo krivo gibanje, imenovano kroženje. Ločevati pa moramo med dvema fizikalnima pojavoma:
vrtenje,
kroženje.
Telo se vrti kot celota. Vrti se okoli premice, ki miruje. Tej premici pravimo os vrtenja.
Če pa opazujemo posamezne točke na vrtečem telesu, pravimo, da krožijo. Gibljejo se namreč po krožnem tiru s središčem v osi vrtenja. Radij kroženja je enak razdalji med krožnico in osjo vrtenja.
V nadaljevanju bomo spoznali obhodni čas, obodno hitrost in frekvenco kroženja. Spoznali in imenovali bomo tudi silo, ki sili telo v krožni tir.
Kroženje je primer krivega gibanja, saj se telo giblje po krivem tiru, krožnici s polmerom r.
Postavimo telo na krožni tir in pustimo, da se enakomerno giblje. Opazimo, da se čez določen čas vrne v začetno lego. Čas, ki je potreben, da se telo po opravljeni krožni poti vrne v začetno točko, imenujemo obhodni čas. Označimo ga s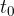 
. Pravimo, da telo v tem času naredi en obhod (krožno pot).
Obhodni čas je čas, ki ga porabi telo pri kroženju, da prepotuje krog s polmerom r. Označujemo ga s 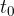, enota pa je s (sekunda).
Pogosteje, kot obhodni čas, v fiziki in tehniki uporabljamo fizikalno količino, imenovano frekvenca. Frekvenca nam pove, kolikokrat se nek pojav ponovi v opazovanem času.
Uporablja se pri vseh ponavljočih (pravimo jim periodična) gibanjih: kroženju, nihanju uteži na vrvici, nihanju strune kitare, valovanju morja, izmeničnih električnih napetosti, radijskih valovih itd.
Frekvenca in obhodni čas sta med sebojno odvisni količini. Večkrat kot telo v opazovanem času obkroži os, manj časa porabi za en obhod. Oziroma, večja kot je frekvenca, manjši je obhodni čas.
Frekvenca kroženja je torej obratno sorazmerna obhodnemu času. Označimo jo z grško črko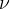 
(izgovorimo "ni").
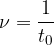
Enota za frekvenco je 
. Imenujemo jo tudi Herz in zapišemo kot Hz.
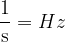
Opazujemo pa lahko tudi število obhodov n, ki jih opravi telo v poljubnem opazovanem intervalu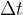 
. V tem primeru izračunamo frekvenco kroženja po enačbi:
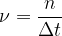
Frekvenca je enaka obratni vrednosti obhodnega časa. Pove nam koliko obhodov na sekundo naredi telo med vrtenjem ali kroženjem. Označimo jo z 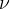, njena enota pa je 1/s ali Hz (Herz).
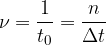
Predmet se enakomerno giblje po krožnici z radijem r. Zveznica r med predmetom in središčem kroga pri kroženju opisuje kot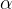 
. Pot s, ki jo naredi v nekem časi t, je enaka dolžini krožnega loka kroga z radijem r:
Gibanje po krožnici
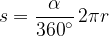
Hitrosti kroženja pravimo obodna ali krožilna hitrost. Izračunamo jo na enak način, kot izračunamo hitrost pri premo enakomernem gibanju:
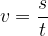
Hitrost lahko izračunamo tako, da za pot vzamemo celoten obseg kroga in pogledamo, koliko časa za to pot potrebuje telo. Čas, ki ga telo potrebuje za en obhod, je enak obhodnemu času.
Izpeljimo torej enačbo za obodno hitrost:
Obhodna hitrost je tem večja, čim večji je radij kroženja in čim krajši je obhodni čas.
Zapišimo hitrost kroženja še v drugi obliki:
Obodna ali krožilna hitrost je hitrost, s katero se predmet giblje po krožnici.
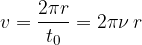
Prvi Newtonov zakon pravi, da se telo giblje enakomerno in premočrtno, če je rezultanta vseh sil, ki delujejo nanj, enaka nič.
Pri enakomernem kroženju se predmet giblje enakomerno, vendar ne premočrtno.
Tir krožečega telesa je kriva črta - krožnica. Na telo torej mora delovati sila, ki ga sili, da vsak trenutek spreminja smer in sledi krožnemu tiru. Ta sila se imenuje centripetalna ali radialna sila. Deluje v smeri radija od predmeta, proti središču kroga.
S poskusom lahko ugotovimo, od česa je odvisna centripetalna sila telesa na vrvici. V ta namen vzamemo električni motor, ki mu lahko spreminjamo frekvenco vrtenja. Na os, preko vrvice in vzmetne tehtnice, pritrdimo krožečo telo z maso m, ki lahko brez trenja drsi po vodoravni podlagi.
Merjenje centripetalne sile z vzmetno tehtnico
Vzmetna tehtnica nam neposredno meri centripetalno silo. Z menjanjem frekvence vrtenja, mase in radija vrtenja lahko raziskujemo, od česa je odvisna sila odvisna. Ugotovitve so naslednje:
centripetalna sila je večja, če je masa telesa večja,
centripetalna sila je večja pri večji frekvenci vrtenja,
centripetalna sila je večja, če je radij vrtenja večji (pri isti frekvenci vrtenja).
Do sedaj smo spoznali silo vrvice, na katero je obešeno krožečo telo. Vrvica omogoča centripetalno silo in s tem kroženje. Če bi se med vrtenjem vrvica strgala, bi telo nadaljevalo pot v smeri hitrosti, ki jo ima v tistem trenutku. To je naravnost, v smeri tangente na krožnico.
Poleg vrvice obstajajo tudi druge sile, ki omogočajo kroženje. Za zdaj omenimo le dve:
sila lepenja,
gravitacija.
