Osebne zbirke


Krožnica je množica točk T v ravnini, ki so od središča S enako oddaljene. Matematično to lahko zapišemo kot:
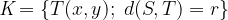
Narišimo krožnico s središčem 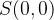 in polmerom
in polmerom  :
:
Točka 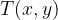 leži na dani krožnici natanko takrat, ko je njena razdalja od izhodišča enaka r. Vidimo, da je polmer, ki ga iščemo, hipotenuza pravokotnega trikotnika
leži na dani krožnici natanko takrat, ko je njena razdalja od izhodišča enaka r. Vidimo, da je polmer, ki ga iščemo, hipotenuza pravokotnega trikotnika 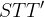 s katetama x in y, zato velja Pitagorov izrek :
s katetama x in y, zato velja Pitagorov izrek :
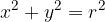
Točka 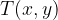 leži na dani krožnici natanko takrat, ko njeni koordinati z in y zadoščata gornji enačbi. Če točka
leži na dani krožnici natanko takrat, ko njeni koordinati z in y zadoščata gornji enačbi. Če točka 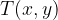 ne leži v prvem kvadrantu je dolžina katet pravokotnega trikotnika enaka
ne leži v prvem kvadrantu je dolžina katet pravokotnega trikotnika enaka 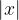 in
in 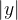 in zaradi kvadriranja dobimo enakovredno enačbo.
in zaradi kvadriranja dobimo enakovredno enačbo.
Enačba krožnice s središčem v koordinatnem izhodišču S(0, 0) in polmerom r je:
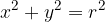
Središče krožnice je lahko tudi zunaj koordinatnega izhodišča npr. v točki 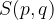 . Narišimo krožnico s središčem
. Narišimo krožnico s središčem 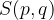 in polmerom r:
in polmerom r:
Točka 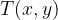 leži na tej krožnici natanko takrat, ko je
leži na tej krožnici natanko takrat, ko je 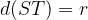 oziroma
oziroma 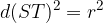 :
:
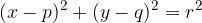
Enačba krožnice s središčem 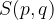 in polmerom
in polmerom  je torej:
je torej:
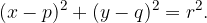
Enačba krožnice s središčem 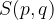 in polmerom r lahko zapišemo tudi v splošni obliki:
in polmerom r lahko zapišemo tudi v splošni obliki:
Enačba krožnice s središčem 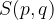 in polmerom r v splošni obliki je torej:
in polmerom r v splošni obliki je torej:
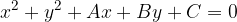
Točka in krožnica sta lahko v različnih medsebojnih legah:
Vidimo, da točka 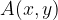 leži na krožnici. Razdalja točke
leži na krožnici. Razdalja točke 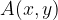 od središča krožnice
od središča krožnice 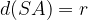 . Kar lahko zapišemo tudi drugače:
. Kar lahko zapišemo tudi drugače:
Točka 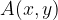 leži na krožnici s polmerom r središčem
leži na krožnici s polmerom r središčem 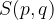 če velja:
če velja:
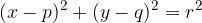
Točka 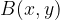 leži v notranjosti kroga. Razdalja točke
leži v notranjosti kroga. Razdalja točke 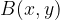 od središča krožnice
od središča krožnice 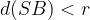 . Zato:
. Zato:
Točka 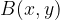 leži v notranjosti kroga s polmerom r središčem
leži v notranjosti kroga s polmerom r središčem 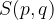 če velja:
če velja:
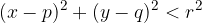
Točka 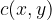 leži v zunanjosti kroga. Razdalja točke
leži v zunanjosti kroga. Razdalja točke 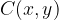 od središča krožnice
od središča krožnice 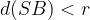 . Zato:
. Zato:
Točka 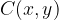 leži v zunanjosti kroga s polmerom r središčem
leži v zunanjosti kroga s polmerom r središčem 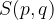 če velja:
če velja:
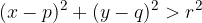
Zanima nas presečišče krožnice 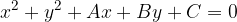 in premice
in premice 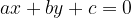
Iz enačbe premice izrazimo eno spremenljivko:
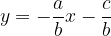
To spremenljivko vstavimo v enačbo krožnice:
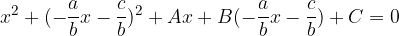
Dobimo kvadratno enačbo:
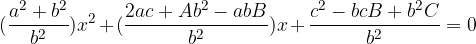
Mogoče so naslednje situacije:
v primeru
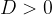
ima kvadratna enačba dve realni rešitvi, zato imata premica in krožnica dve skupni točki.
v primeru
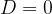
ima kvadratna enačba eno realno rešitev, zato imata premica in krožnica eno skupno točko; premica je tangenta na krožnico.
v primeru
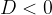
nima ta kvadratna enačba nobenih realnih rešitev zato premica in krožnica nimata skupnih točk.