Osebne zbirke


Krog je geometrijski lik, obdan s sklenjeno krivuljo.
Krog sestavlja množica točk, zbranih okoli točke na sredini, ki jo imenujemo središče. Središče označimo z veliko tiskano črko 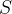 .
.
Množica točk je navzven omejena s sklenjeno krivuljo, ki jo imenujemo krožnica.
Krožnica je množica točk v ravnini, ki so enako oddaljene od dane točke 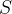 .
.
Vse točke na krožnici so od središča oddaljene za točno določeno vrednost. Razdaljo od središča do katere koli točke na krožnici imenujemo polmer. Polmer označimo z malo tiskano črko  .
.
Daljico, ki povezuje dve točki na krožnici in poteka skozi središče, imenujemo premer. Premer je dvakratnik polmera. Označimo ga z malo črko 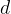 .
.
Premer kroga je dvakratna vrednost polmera:
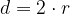
Obseg kroga je dolžina krožnice. Označimo ga z malo tiskano črko 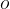 .
.
Pri računanju obsega kroga se srečamo z do sedaj neznanim številom 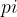 , ki ga označujemo z malo grško črko
, ki ga označujemo z malo grško črko 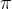 .
.
Število iz zgornjega primera, ki pove, kolikokrat je obseg kroga večji od njegovega premera, imenujemo 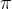 .
.
Obseg krožnice je torej zmnožek števila 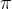 in premera
in premera 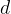 :
:
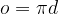
Če upoštevamo, da je premer 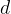 dvakratna vrednost polmera
dvakratna vrednost polmera  , pa obseg krožnice lahko zapišemo kot:
, pa obseg krožnice lahko zapišemo kot:
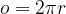
Obseg krožnice izračunamo po enačbi:
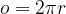
kjer je 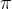 konstanta,
konstanta,  pa polmer kroga.
pa polmer kroga.
Če imamo podan premer 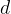 , lahko obseg izračunamo po enačbi:
, lahko obseg izračunamo po enačbi:
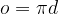
Število 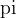 v računu običajno pustimo kar tako, kot faktor
v računu običajno pustimo kar tako, kot faktor 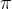 . Njegove natančne vrednosti namreč ne moremo napisati lepše, saj je to število z neskončnim številom decimalk:
. Njegove natančne vrednosti namreč ne moremo napisati lepše, saj je to število z neskončnim številom decimalk:
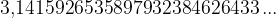
Če pa želimo izvedeti na primer, koliko centimetrov meri obseg kroga, potem pa za 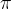 v račun vnesemo približek
v račun vnesemo približek 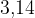 ali pa ulomek
ali pa ulomek 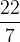 in izračunamo približen rezultat.
in izračunamo približen rezultat.
Število 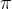 je neskončno decimalno število. Za njegov približek v računu lahko uporabimo eno od vrednosti:
je neskončno decimalno število. Za njegov približek v računu lahko uporabimo eno od vrednosti:
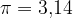
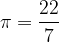
Ploščina kroga je površina ploskve, omejene s krožnico. Označimo jo z malo tiskano črko 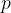 .
.
Ploščino kroga izračunamo po formuli:
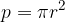
kjer je 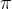 konstanta,
konstanta,  pa polmer kroga.
pa polmer kroga.
Krožni lok je del krožnice, omejen z dvema točkama. Označimo ga z malo tiskano črko 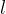 .
.
Če krajišči krožnega loka povežemo s središčem, dobimo kot, katerega vrh leži v središču kroga, njegova kraka pa sta polmera. Ta kot imenujemo središčni kot.
Če si izberemo večji središčni kot 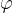 , bo ta kot opisal večji del krožnice.
, bo ta kot opisal večji del krožnice.
Če vzamemo 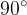 , kar je
, kar je  polnega kota, potem nam ta kot opiše ravno
polnega kota, potem nam ta kot opiše ravno  krožnice:
krožnice:
Če vzamemo kot 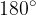 , kar je
, kar je  polnega kota, potem nam ta kot opiše
polnega kota, potem nam ta kot opiše  krožnice:
krožnice:
Opazimo torej da, večji kot je središčni kot, večji je tudi del krožnice. Natančneje, delež polnega kota je enak deležu krožnice:
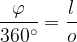
Če poznamo središčni kot in obseg krožnice, lahko izračunamo dolžino krožnega loka:
Dolžino krožnega loka izračunamo po enačbi
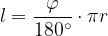
kjer je:
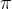 konstanta s približno vrednostjo
konstanta s približno vrednostjo 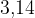 ali
ali 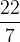 ,
,
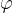 središčni kot v stopinjah,
središčni kot v stopinjah,
 pa polmer kroga.
pa polmer kroga.
Krožni izsek je množica točk, omejena s krožnim lokom in polmeroma do krajišč krožnega loka.
Če si izberemo večji središčni kot 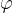 , bo ploščina krožnega izseka večja.
, bo ploščina krožnega izseka večja.
Če vzamemo 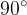 , kar je
, kar je  polnega kota, ploščina krožnega izseka obsega ravno
polnega kota, ploščina krožnega izseka obsega ravno  kroga:
kroga:
Če vzamemo 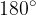 , kar je
, kar je  polnega kota, ploščina krožnega izseka obsega ravno
polnega kota, ploščina krožnega izseka obsega ravno  kroga:
kroga:
Opazimo torej da, večji kot je središčni kot, večji je tudi del kroga. Natančneje, delež polnega kota je enak deležu ploščine kroga:
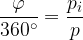
pri čemer je 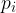 ploščina krožnega izseka.
ploščina krožnega izseka.
Iz omenjenega razmerja lahko izpeljemo enačbo za ploščino krožnega izseka:
Ploščino krožnega izseka izračunamo po enačbi
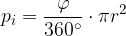
kjer je:
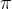 konstanta s približno vrednostjo
konstanta s približno vrednostjo 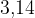 ali
ali 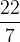 ,
,
 središčni kot v stopinjah,
središčni kot v stopinjah,
 pa polmer kroga.
pa polmer kroga.