Osebne zbirke


Kvader je geometrijsko telo, ki je omejeno s šestimi pravokotnimi ploskvami, ki se stikajo v robovih. Postavljene so pravokotno druga na drugo. Po dve nasprotni ploskvi sta vzporedni in skladni.
Kvader je naš vsakdanji sopotnik in prav je, da o njem zvemo nekaj več.
Poglejmo vse značilne elemente kvadra.
Oglišče v kvadru je stičišče treh njegovih robov. Oglišča označujemo z velikimi tiskanimi črkami A, B, C, D, E, F, G in H, ki si sledijo v nasprotni smeri urnega kazalca (v matematiki je to pozitivna smer).
Rob je daljica, ki omejuje vsako mejno ploskev v telesu in povezuje sosednji oglišči. Kvader ima 12 robov. Najlažje jih je določiti, če vzamemo, da so:
štirje spodaj (rob AB, rob BC, rob CD in rob AD),
štirje zgoraj (rob EF, rob FG, rob GH in rob EH) in
štirje stranski robovi (rob AE, rob BF, rob CG in rob DH).
Tako kot stranice geometrijskih likov (trikotnik, pravokotnik, šestkotnik...), tudi robove kvadra označujemo z majhnimi pisanimi črkami angleške abecede.
Pozorni bodimo na razlike v poimenovanju elementov v likih in telesih. Da se ne zmotimo pri poimenovanju, si zapomnimo:
Geometrijski liki, kot so trikotniki, štirikotniki, trapezi, deltoidi, so omejeni s stranicami.
Geometrijska telesa, kot sta kocka in kvader, so omejena s ploskvami. Skupni del dveh sosednjih ploskev pa imenujemo rob.
Ploskev, na kateri kvader leži, imenujemo osnovna ploskev kvadra. Kvader ima dve osnovni ploskvi, podobno kot kocka. Druga je nasproti prvi, na vrhu kvadra.
Običajno je osnovna ploskev pravokotnik. Če pa je v kvadru dolžina enaka širini, potem je osnovna ploskev kvadrat.
Osnovni rob je daljica, ki povezuje sosednji oglišči osnovne ploskve. Na sliki so osnovni robovi označeni z modro barvo.
Stranske ploskve kvadra so ploskve, ki so pravokotne na osnovno ploskev. Zaradi preglednosti sta na spodnji sliki označeni le dve sosednji stranski ploskvi.
Po dve in dve nasprotni stranski ploskvi sta skladni in vzporedni. Vse štiri pa tvorijo plašč kvadra.
Višina ali stranski rob je najkrajša daljica, ki povezuje oglišča osnovnih ploskev. Na sliki so stranski robovi označeni z modro barvo, vse druge oznake (oglišča, dolžina in širina kvadra) so izpuščene.
Stranskim robovom prej še nismo namenjali posebne pozornosti. Pri obravnavi kvadra pa stranski rob ločujemo od osnovnega roba.
Ploskovna diagonala povezuje nasprotni oglišči katerekoli mejne ploskve. Običajna oznaka za ploskovno diagonalo kvadra je majhna črka 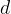 z indeksom:
z indeksom: 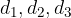 .
.
Vsaka mejna ploskev kvadra ima dve enako dolgi diagonali. Presečišče diagonal je točno na njuni polovici. Ploskovna diagonala razdeli mejno ploskev na dva enaka pravokotna trikotnika. Hkrati v tako nastalemu pravokotnemu trikotniku predstavlja hipotenuzo, robova pa sta kateti.
Telesna diagonala kvadra povezuje nasprotni oglišči vzporednih ploskev. Običajna oznaka za telesno diagonalo kvadra je majhna črka d.
Kvader ima štiri telesne diagonale:
če je začetna točka diagonale oglišče A, potem je končna točka te diagonale oglišče G,
če je začetna točka diagonale oglišče B, potem je končna točka te diagonale oglišče H,
če je začetna točka diagonale oglišče C, potem je končna točka te diagonale oglišče E,
če je začetna točka diagonale oglišče D, potem je končna točka te diagonale oglišče F,
Presečišče telesnih diagonal je znotraj kvadra in jih razpolavlja.
Pri fiziki je včasih potrebno ugotoviti, kje je težišče kakšnega telesa. Ko je telo kvader, potem je njegovo težišče ravno presečišče telesnih diagonal.
V kvadru se pogosto uporablja Pitagorov izrek za računanje ploskovnih diagonal ali telesnih diagonal.
Na spodnji sliki vidimo: rob AB (dolžina kvadra) in rob BC (širina kvadra) sta kateti, diagonala 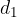 osnovne ploskve pa je hipotenuza pravokotnega trikotnika.
osnovne ploskve pa je hipotenuza pravokotnega trikotnika.
Če hočemo izračunati dolžino ploskovne diagonale AC ali BD oziroma 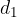 , moramo sešteti kvadrata dolžine in širine in na koncu izračunati koren rezultata, ki ga dobimo.
, moramo sešteti kvadrata dolžine in širine in na koncu izračunati koren rezultata, ki ga dobimo.
Diagonala osnovne ploskve 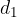 in višina
in višina 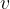 sta kateti, telesna diagonala
sta kateti, telesna diagonala 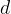 pa hipotenuza pravokotnega trikotnika.
pa hipotenuza pravokotnega trikotnika.
Da dobimo površino kvadra, moramo sešteti ploščine vseh njegovih ploskev. Govorimo o skupno šestih ploskvah, ki ga omejujejo:
dveh osnovnih ploskvah in
štirih stranskih ploskvah.
Te ploskve so v splošnem pravokotniki, lahko pa so tudi kvadrati.
Za računanje površine kvadra moramo torej znati izračunat ploščino pravokotnika in kvadrata.
Formulo za površino kvadra bomo izpeljali tako, da bomo najprej narisali mrežo kvadra. Na mreži označimo tudi vse robove.
Vidimo, da je mreža sestavljena iz treh parov skladnih pravokotnikov. Na spodnji sliki označimo skladne pravokotnike z isto barvo. Če mrežo izrežemo iz papirja in jo sestavimo v kvader, potem enako obarvani ploskvi ležita ena nasproti druge.
Ploščino kvadra lahko še bolj nazorno pokažemo s sliko, na kateri je mreža kvadra narisana v milimetrski kvadratni mreži. Na spodnji sliki vidimo mrežo kvadra v kvadratni mreži. Označene so tudi ploščine vseh pravokotnikov - ploskev kvadra.
Za površino 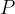 kvadra torej seštejemo vse ploščine pravokotnikov:
kvadra torej seštejemo vse ploščine pravokotnikov:
Obrazec za površino kvadra:
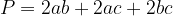
pogosto zapišemo v obliki z izraženo dvojko:
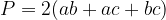
Prostornina kvadra je velikost prostora, ki je ujet med njegove stene.
Dokler še ne znamo izračunati prostornine kvadra, si lahko pomagamo s kockami enakih velikosti. Takšnim kockam običajno rečemo enotske kocke. Prostornina ene kocke je odvisna od dolžine njenega robu. Če ima kocka rob dolg en centimeter, potem je njena prostornina en kubični centimeter. S takšnimi kockami lahko izmerimo prostornino kvadra.
Kocke lahko zlagamo na različne načine. Če zložimo tri kocke v vrsto, dobimo kvader s prostornino, ki je enaka prostornini treh kock. Oziroma, če uporabimo enake enotske kocke kot prej, je prostornina kvadra enaka trem kubičnim centimetrom.
Še naprej se igramo in kvadru, sestavljenem iz treh kock, dodamo še tri kocke (glej sliko). Kvader, ki nastane na ta način, ima prostornino enako prostornini šestih kock.
Nič drugače ni, če tri kocke postavimo zraven prejšnjih treh. Tudi v tem primeru dobimo kvader. Njegova prostornina je tudi enaka prostornini šestih kock.
Prostornini rečemo tudi volumen. Za prostornino vzamemo oznako 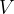 . Iz gornjega primera lahko izpeljemo obrazec za računanje prostornine kvadra. Dobimo jo tako, da pomnožimo dolžino, širino in višino kvadra.
. Iz gornjega primera lahko izpeljemo obrazec za računanje prostornine kvadra. Dobimo jo tako, da pomnožimo dolžino, širino in višino kvadra.
Obrazec za prostornino kvadra:
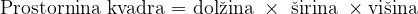
Oziroma:
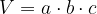
Znak "krat" lahko opustimo in dobimo:
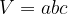
Predstavljajmo si, da kvader presekamo točno po eni izmed njegovih ploskovnih diagonal. Tako opišemo ploskev, ki ji pravimo diagonalni presek kvadra. Diagonalni presek kvadra je vedno nek pravokotnik, ki ima za:
dolžino: eno izmed diagonal,
širino: eno izmed treh razsežnosti kvadra (dolžino ali širino ali višino).
Na spodnjih slikah lahko vidimo vse tri različne diagonalne preseke v kvadru. Dobimo jih tako, da kvader presekamo po različnih ploskovnih diagonalah.
Na gornji sliki je diagonalni presek pravokotnik z dolžino, ki je enaka diagonali osnovne ploskve kvadra, in širino, ki je enaka višini kvadra.
Na gornji sliki je diagonalni presek pravokotnik z dolžino, ki je enaka dolžini kvadra, in širino, ki je enaka stranski diagonali kvadra.
Na gornji sliki je diagonalni presek pravokotnik z dolžino, ki je enaka stranski diagonali kvadra, in širino, ki je enaka širini kvadra.