Prijava z e-naslovom
Prijava brez gesla
Kvadrat števila že poznamo.
Poglejmo si, kako pa zgleda kvadrat dvočlenika:
V nadaljevanju si poglejmo, kako ga izračunamo.
Do kvadrata dvočlenika pridemo po enakem postopku kot med seboj množimo veččlenike. Dvočlenik kvadriramo tako, da ga množimo samega s seboj.
Pri kvadriranju dvočlenika smo dobili tričlenik. Pri tem smo produkt dveh členov:
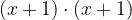
preoblikovali v vsoto treh členov:
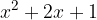
Postopku preoblikovanja produkta v vsoto pravimo razčlenjevanje.
Iz zgornjega primera lahko razberemo pravilo za izračun kvadrata dvočlenika. V rezultatu vidimo, da za tričlenik velja:
Prvi člen tričlenika dobimo tako, da kvadriramo prvi člen začetnega dvočlenika;
Drugi (vmesni) člen tričlenika je vsota dveh enakih produktov - produktov prvega in drugega člena dvočlenika;
Tretji člen tričlenika dobimo tako, da kvadriramo drugi člen dvočlenika.
Ko izračunamo kvadrat dvočlenika, vedno dobimo tričlenik.
Izpeljimo splošno formulo za kvadriranje kateregakoli dvočlenika. Kvadrirajmo dvočlenik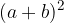 
, pri čemer sta lahko a in b poljubni števili (tudi negativni).
Izračunajmo:
Ker sta števili a in b poljubni števili, velja zgornji rezultat splošno, v vsakem primeru. a predstavlja prvi člen dvočlenika, b pa drugi člen. Z besedami lahko oblikujemo pravilo za kvadrat dvočlenika kot:
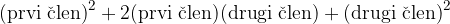
Oziroma v matematični obliki z obrazcem (formulo) za kvadrat dvočlenika.
Pravilo za izračun kvadrata dvočlenika:
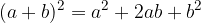
Preoblikovanje produkta členov v vsoto ali razliko členov imenujemo razčlenjevanje.
Poglejmo si še en primer, ko je eno od števil negativno.
Če je v dvočleniku eden od členov negativen, potem kot rezultat dobimo tričlenik, ki ima drugi člen negativen.
