Osebne zbirke


Kvadratna enačba je enačba, v kateri nastopa neznanka v največ v drugi potenci.
S smotrnim urejanjem se dajo vse kvadratne enačbe prevesti v splošno obliko kvadratne enačbe

kjer so koeficienti a, b in c poljubna realna števila. Koeficient a imenujemo koeficient kvadratnega člena ali vodilni koeficient, b koeficient linearnega člena in c stalni, svobodni, prosti, ali konstantni člen.
Koeficient a ne more biti enak 0, ker potem enačba ni več kvadratna.
Glede kvadratnih enačb velja takoj v začetku naglasiti, da jih za razliko od linearnih enačb, kjer pišemo stalni člen na desni strani, urejujemo dosledno tako, da je desna stran enaka 0, na levi strani pa razvrstimo člene po padajočih potencah.
Podano imamo enačbo:
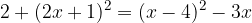
Uredimo enačbo:
Podano imamo enačbo:
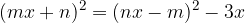
Uredimo enačbo:
Kvadratna enačba ima dve rešitvi, ki ju izračunamo po obrazcu:
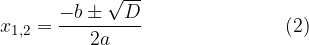
pri čemer je D diskriminanta, ki jo izračunamo po obrazcu:

Za rešitvi kvadratne enačbe imamo kar šest različnih izrazov: rešitvi kvadratne enačbe = ničli kvadratne enačbe = korena kvadratne enačbe = ničli kvadratne funkcije = presečišče kvadratne funkcije z osjo x = presečišče kvadratne funkcije z abscisno osjo.
Število in značaj rešitev kvadratne enačbe je odvisen od diskriminante D:
če je 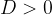 , ima enačba dve različni realni rešitvi
, ima enačba dve različni realni rešitvi
če je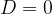 , ima enačba eno samo dvojno realno rešitev
, ima enačba eno samo dvojno realno rešitev 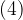
če je 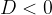 , enačba nima realnih rešitev
, enačba nima realnih rešitev
Enačba ima dve kompleksni rešitvi (konjugirano kompleksni števili), ki ju bomo obravnavali v poglavju Kompleksna števila.
Nekaj primerov reševanja kvadratnih enačb:
Imamo kvadratno enačbo
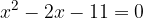
Koeficienti kvadratne enačbe so: a = 1, b = -2 in c = -11. Kvadratno enačbo rešimo tako, da najprej izračunamo diskriminanto po obrazcu :
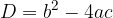
Vrednost diskriminante je 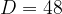 . Ker je diskriminanta večja od 0, vemo, da ima kvadratna enačba dve različni realni rešitvi. Izračunamo ju s pomočjo obrazca:
. Ker je diskriminanta večja od 0, vemo, da ima kvadratna enačba dve različni realni rešitvi. Izračunamo ju s pomočjo obrazca:
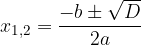
Rešitvi kvadratne enačbe sta:
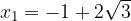 in
in 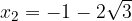
Imamo kvadratno enačbo
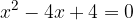
Koeficienti kvadratne enačbe so: a = 1, b = -4 in c = 4. Kvadratno enačbo rešimo tako, da najprej izračunamo diskriminanto po obrazcu : 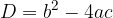
Vrednost diskriminante je 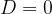 . Ker je diskriminanta enaka 0, vemo, da ima kvadratna enačba eno samo dvojno realno rešitev. Izračunamo jo s pomočjo obrazca:
. Ker je diskriminanta enaka 0, vemo, da ima kvadratna enačba eno samo dvojno realno rešitev. Izračunamo jo s pomočjo obrazca: 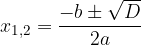
Rešitvi kvadratne enačbe sta: 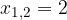
Imamo kvadratno enačbo
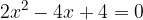
Koeficienti kvadratne enačbe so: a = 2, b = -4 in c = 4. Kvadratno enačbo rešimo tako, da najprej izračunamo diskriminanto po obrazcu : 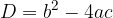
Vrednost diskriminante je 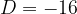 . Ker je diskriminanta negativna , enačba nima realnih rešitev. Enačba ima dve kompleksni rešitvi (konjugirano kompleksni števili), ki se ju bomo naučili računati v poglavju Kompleksna števila.
. Ker je diskriminanta negativna , enačba nima realnih rešitev. Enačba ima dve kompleksni rešitvi (konjugirano kompleksni števili), ki se ju bomo naučili računati v poglavju Kompleksna števila.
V predhodnjem poglavju smo izvedeli, da lahko s pomočjo dveh obrazcev:
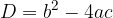
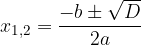
rešimo katerokoli kvadratno enačbo. Do rešitev ali korenov nekaterih posebnih oblik kvadratnih enačb pa lahko pridemo tudi po enostavnejših in hitrejših postopkih s pomočjo razstavljanja, zato si jih oglejmo:
V primeru, ko je linearni člen b = 0, se splošna oblika kvadratne enačbe preoblikuje v:

Rešitev izpeljemo tako, da kvadratno enačbo najprej pretvorimo v ničelno ali faktorizirano obliko. V množici realnih števil se da enačbo zapisati v ničelni obliki samo v primeru, če imata a in c nasprotna predznaka. Kako se enačba zapiše v ničelni obliki, če imata a in c enaka predznaka, je obravnavano v poglavju Kompleksna števila.
Rešimo prvo (linearno) enačbo:
Rešimo drugo (linearno) enačbo:
Imamo enačbo:
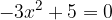
Rešitev izpeljemo tako, da kvadratno enačbo najprej pretvorimo v ničelno ali faktorizirano obliko:
Rešimo prvo (linearno) enačbo:
Rešimo drugo (linearno) enačbo:
V primeru, ko je stalni člen c = 0, se splošna oblika kvadratne enačbe preoblikuje v:

Rešitev izpeljemo tako, da kvadratno enačbo najprej pretvorimo v ničelno ali faktorizirano obliko:
Prva enačba je že rešena, zato rešimo drugo (linearno) enačbo:
Imejmo enačbo:
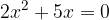
Rešitev izpeljemo tako, da kvadratno enačbo najprej pretvorimo v ničelno ali faktorizirano obliko:
Prva enačba je že rešena, zato rešimo drugo (linearno) enačbo:
V primeru, ko je vodilni člen a = 1, se splošna oblika kvadratne enačbe preoblikuje v:

Kvadratni tričlenik oblike 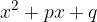 najprej razstavimo na podlagi istovetne enačbe, s pomočjo katere jo pretvorimo v ničelno ali faktorizirano obliko:
najprej razstavimo na podlagi istovetne enačbe, s pomočjo katere jo pretvorimo v ničelno ali faktorizirano obliko:

Razstavljanje je možno samo, če se da q zapisati kot produkt dveh faktorjev m in n, katerih vsota je enaka p.
Razstavljeno enačbo rešimo:
Rešimo prvo (linearno) enačbo:
Rešimo drugo (linearno) enačbo:
Podano imamo enačbo:
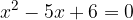
Koeficienti so a = 1, p = - 5 in q = 6
Podano enačbo razstavimo po obrazcu 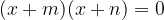 in rešimo:
in rešimo:
Rešimo prvo (linearno) enačbo:
Rešimo drugo (linearno) enačbo:
Splošno obliko kvadratne enačbe: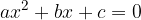 zapišemo v ničelni obliki s pomočjo zapisa:
zapišemo v ničelni obliki s pomočjo zapisa:
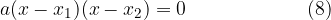
kjer so:
a koeficient kvadratnega člena ali vodilni koeficient in
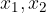 rešitvi kvadratne enačbe, ki ju izračunamo po obrazcu:
rešitvi kvadratne enačbe, ki ju izračunamo po obrazcu:
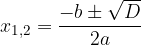
pri čemer je D diskriminanta, ki jo izračunamo po obrazcu:
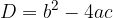
Za ničelno obliko imamo dva različna izraza: ničelna oblika = faktorizirana oblika. Postopek imenujemo razstavljanje ali faktoriziranje.
Vse kvadratne enačbe lahko zapišemo v ničelni obliki s pomočjo obrazca za izračun rešitev kvadratne enačbe (tudi posebne oblike kvadratnih enačb iz predhodnega poglavja).