Prijava z e-naslovom
Prijava brez gesla
Korenjenje je matematična operacija, ki deluje obratno od potenciranja (pravimo, da je obratna operacija potenciranju). Tipičen primer, ko potrebujemo korenjenje, je reševanje kvadratnih enačb. Npr.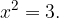 
Korenjenje zapišemo s simbolom:
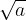
kar preberemo: kvadratni koren iz a. Znak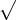 
imenujemo korenski znak, število 
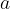pa korenjenec.
Definicija: kvadratni koren danega števila 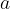, kjer je 
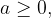je tako nenegativno število 
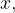da je:
Računanje na pamet
Kadar v korenjencu prepoznamo kvadrat kakega števila, lahko iskani kvadratni koren kar zapišemo.
Računanje s kalkulatorjem
Kadar vrednosti kvadratnih korenov ne znamo izračunati na pamet, korene v rezultatih ohranimo. Če pa želimo eksplicitno zapisati številčni rezultat, si pomagamo s kalkulatorjem.
Rešimo kvadratno enačbo: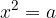 
Enačba 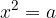ima v množici realnih števil:
za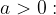 
dve rešitvi: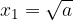 
in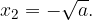 
Namreč produkt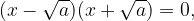 
ko je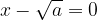 
ali ko je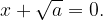 
za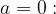 
eno dvakratno rešitev: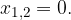 
Rešujemo enačbo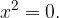 
za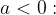 
nima rešitev.
Ustavimo se že pri drugem koraku reševanja enačbe, saj pod korenom ne moremo imeti negativno število oziroma 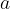ne moremo zapisati kot 
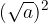, če je 
.
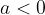Za računanje s kvadratnimi koreni veljajo naslednja pravila:
Kvadrat kvadratnega korena nenegativnega števila 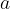je število samo:
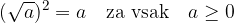
Kvadratni koren kvadrata realnega števila 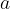je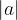 
:
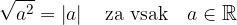
Kvadratni koren produkta dveh (ali več) nenegativnih števil je enak produktu kvadratnih korenov teh dveh števil:
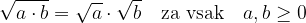
Kvadratni koren količnika dveh števil je enak količniku kvadratnih korenov teh števil, pri čemer je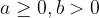 
:
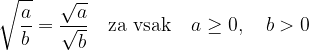
Število delno korenimo tako, da ga zapišemo kot produkt dveh faktorjev, od katerih enega lahko korenimo.
Racionalizirati imenovalec pomeni ulomek razširiti tako, da v imenovalcu ni korena.
Ulomke bomo preoblikovali v ulomke z enako vrednostjo, in sicer tako, da jih bomo pomnožili z ulomkom, katerega vrednost bo enaka 1, tako da se vrednost prvotnega izraza ne bo spremenila. Kako zapisati število 1 pa je odvisno od ulomka, ki ga racionaliziramo.
Postopek racionalizacije si poglejmo skozi naslednja primera.
