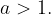Prijava z e-naslovom
Prijava brez gesla
Z limito v neskončnosti opišemo obnašanje funkcij in njihovih grafov daleč proč od koordinatnega izhodišča, ko neodvisna spremenljvka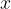 
raste prek vseh meja v pozitivno ali negativno smer.
Zapišemo jo kot:
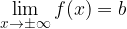
Za lažje razumevanje sledeče definicije se spomnimo:
Okolica točke.
Okolica točke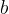 
je odprt interval okoli 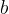s središčem v 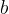. Odprti interval 
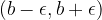imenujemo 
(epsilon) okolica števila 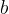. Širina tega intervala je odvisna od pozitivnega števila , ki je ponavadi zelo majhen.
Vrednost M
Vrednost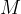 
je realna vrednost, ki leži na 
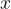-osi. Pri limiti v neskončnosti predstavlja mejo, čez katero vse funkcijske vrednosti 
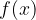ležijo v -okolici, ko se 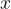približuje vrednosti v neskončnosti.
Limita v neskončnosti se nahaja v točki 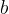, ko gre 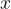v neskočnost, če za vsak izbran 
najdemo tako realno število 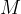, da se vsi 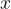, ki so večji od 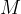, preslikajo v 
-okolico točke .
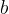Velja, da
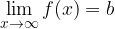
če za vsak 
obstaja tako realno število 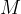, da velja:
če je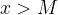 
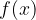, je v -okolici točke .
Primer limite v neskončnosti
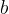Imejmo funkcijo 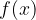. Če velja:
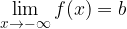
potem povsem enakovredno velja tudi:
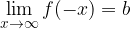
Za limite v neskončnosti pri zrcalnih grafih (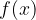 in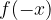 
sta simetrična glede na y-os) velja:
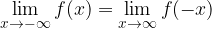
V nadaljevanju se bomo osredotočili na racionalne funkcije, kjer je stopnja polinoma v števcu maksimalno za 1 večja od stopnje polinoma v imenovalcu. Ta pogoj postavljamo zato, ker se želimo omejiti na največ linearne asimptote.
Velja naslednje:
Graf funkcije se daleč proč od koordinatnega izhodišča približuje abscisni osi.
Iz tega sledi:
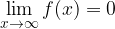
Velja naslednje:
Graf funkcije se daleč proč od koordinatnega izhodišča približuje vodoravni asimptoti z enačbo:
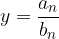
kjer sta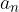 
in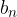 
vodilna koeficienta teh dveh polinomov.
Iz tega sledi:
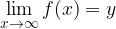
Velja naslednje:
Vrednosti take racionalne funkcije rastejo prek vseh meja, ko gre 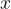v neskončnost. Graf se približuje poševni asimptoti.
Velja tudi, da večji kot je 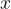, manjša je razdalja med funkcijo in poševno asimptoto. Kar pomeni, da večji, ko je 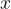, manjša je razlika med vrednostjo racionalne funkcije in vrednostjo linearne funkcije 
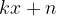, to je kvocienta števca in imenovalca.
Vrednost 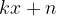predstavlja v tem primeru enačbo poševne asimptote, ki jo dobimo na naslednji način:
Imejmo racionalno funkcijo oblike:
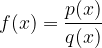
Za izračun poševne asimptote moramo zdeliti polinom v števcu -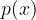 
s polinomom v imenovalcu - 
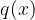. Dobimo:
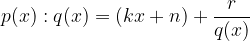
Za ostanek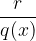 
vemo, da večji kot je 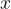, manjši je ta člen. Torej, ko gre 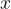v neskončnost gre ta člen proti nič.
Iz tega sledi, da je enačba poševne asimptote:
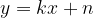
Z naraščanjem neodvisne spremenljivke 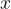postaja razlika med vrednostjo funkcije 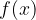in kvocientom 
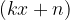vse manjša, torej limitira proti nič:
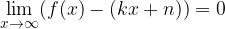
Spomnimo se oblike eksponentne funkcije:
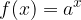
Vemo, da limita v neskončnosti v neki vrednosti a obstaja samo, kadar se funkcija z naraščanjem vrednosti x približuje tej vrednosti a, zato moramo biti pozorni na predznak neskončnosti v katero 'pošljemo' x. Iz tega sledi, da zgornja trditev velja le v primerih kadar je izpolnjen eden izmed naslednjih pogojev:
Za limito eksponentne funkcije velja
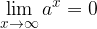
če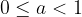 
oziroma
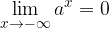
če 
