Osebne zbirke


Eksponentna funkcija, ki jo že poznamo, je bijektivna. Zato lahko poiščemo njeno inverzno funkcijo.
Inverzna funkcija eksponentne funkcije je logaritemska funkcija z osnovo a večjo od 0 in različno od 1 in logaritmandom x večjim od 0:
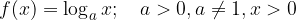
Logaritemska funkcija ne more imeti osnove 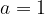 , saj bi v tem primeru dobili vzporednico ordinatni osi skozi točko
, saj bi v tem primeru dobili vzporednico ordinatni osi skozi točko 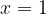 , torej linearno funkcijo.
, torej linearno funkcijo.
Grafično dobimo logaritemsko funkcijo, če eksponentno funkcijo prezrcalimo preko simetrale lihih kvadrantov oziroma premice 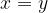 .
.
Tako kot eksponentne funkcije, tudi logaritemske funkcije glede na velikost osnove a razdelimo v dve družini:
osnova je večja od 1:
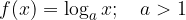
osnova je med 0 in 1:
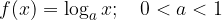
Sedaj si na konkretnih primerih poglejmo po en graf iz vsake družine.
Sedaj lahko čisto na kratko primerjamo grafa funkcij obeh družin, saj bomo lastnosti podrobneje predstavili v poglavju lastnosti. Obe funkciji:
imata enako definicijsko območje, zalogo vrednosti, navpično asimptoto,
nista sodi in ne lihi,
potekata skozi točko 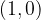 ,
,
sta bijektivni,
sta zrcalni glede na abscisno os.
Prva od njiju je naraščajoča, druga padajoča.
Oblika logaritemske funkcija vpliva na lastnosti funkcije in na izgled njenega grafa. Obravnavali bomo dve obliki logaritemske funkcije, osnovno in splošno.
Zaradi lastnosti funkcij, ki so skupne nekaterim logaritemskim funkcijam, imenujmo logaritemsko funkcijo
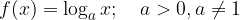
osnovna logaritemska funkcija, saj funkcija ni pomnožena s konstanto, ne vsebuje prostega člena in ni konstantna.
Splošna obliko logaritemske funkcije je naslednja:
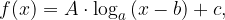
kjer A pomeni razteg ali skrčitev grafa v smeri osi y, b premik v smeri osi x, c pa je prosti člen, ki pomeni premik grafa v smeri osi y.
Če je b < 0 graf premaknemo za b enot v levo, če je pa b > 0 graf premaknemo za b enot v desno.
Če je c < 0 graf premaknemo za c enot navzdol, če je pa c > 0 graf premaknemo za c enot navzgor.
Pri premiku grafa za b enote v levo ali desno, ne smemo pozabiti, da se za b enote v levo ali desno premakne tudi navpična asimptota funkcije.
Ker se lastnosti logaritemske funkcije ločijo glede na to, ali je osnova večjo od 1 ali pa se nahaja med 0 in 1, bomo oba primera obravnavali posebej. Večji poudarek bomo namenili osnovnim logaritemskim funkcijam, saj imajo skupne lastnosti, ne glede na vrednost osnove a.
Lastnosti eksponentne funkcije je lažje razumeti, če si jo predstavljamo, zato si pomagajmo z grafi.
Definicijsko območje eksponentne funkcije postane zaloga vrednosti logaritemske funkcije, zaloga vrednosti eksponentne funkcije pa definicijsko območje logaritemske funkcije.
Definicijsko območje logaritemske funkcije z osnovo večjo od 1 je množica pozitivnih realnih števil:
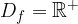
Zaloga vrednosti je celotna množica realnih števil:
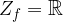
Logaritemska funkcija z osnovo a >1, je na celotnem definicijskem območju strogo naraščajoča, saj za poljubni dve vrednosti:
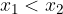
velja
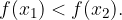
Za vrednosti spremenljivke x>0, graf logaritemske funkcije narašča od minus neskončnosti proti neskončnosti, zato funkcija navzdol in navzgor ni omejena.
Logaritemske funkcije so navzdol in navzgor neomejene.
Ko vrednosti spremenljivke x padajo proti minus neskončnosti, se graf splošne logaritemske funkcije
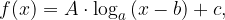
približuje premici, ki ji pravimo navpična asimptota, in ki je enaka koeficientu b:
Navpična asimptota:
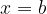
V primeru osnovne oblike, je koeficient b enak 0. Takrat je navpična asimptota funkcije ordinatna os.
Konstanta A in prosti člen c na navpično asimptoto ne vplivata.
Funkcija je injektivna, ker se vsak x preslika v natanko en y.
Funkcija je surjektivna, ker vsakemu y pripada vsaj en x, ki se vanj preslika.
Funkcija je bijektivna, saj je injektivna in surjektivna.
Pri določanju injektivnosti in surjektivnosti si lahko pomagamo tudi z vzporednicami abscisni osi. Več o tem lahko preberete v gradivu Funkcije in njene lastnosti.
Vsem grafom osnovne logaritemske funkcije je skupno presečišče z abscisno osjo (ničla funkcije), to je točka 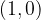 .
.
V primeru splošne oblike pa naš graf funkcije več ne poteka skozi točko 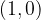 .
.
Logaritemska funkcija 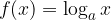 ni soda ker:
ni soda ker:
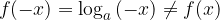
Logaritemska funkcija 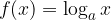 ni liha ker:
ni liha ker:
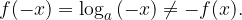
Večji poudarek bomo tudi tukaj namenili osnovnim logaritemskim funkcijam, saj imajo skupne lastnosti, ne glede na vrednost osnove a.
Definicijsko območje eksponentne funkcije postane zaloga vrednosti logaritemske funkcije, zaloga vrednosti eksponentne funkcije pa definicijsko območje logaritemske funkcije.
Definicijsko območje logaritemske funkcije z osnovo med 0 in 1 je množica pozitivnih realnih števil:
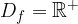
Zaloga vrednosti je celotna množica realnih števil:
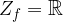
Logaritemska funkcija z osnovo med 0 in 1, je na celotnem definicijskem območju strogo padajoča, saj za poljubni dve vrednosti:
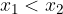
velja
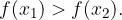
Za vrednosti spremenljivke x>0, graf logaritemske funkcije ves čas pada, zato funkcija navzdol in navzgor ni omejena.
Logaritemske funkcije so navzdol in navzgor neomejene.
Ko vrednosti spremenljivke x padajo proti minus neskončnosti, se graf splošne logaritemske funkcije
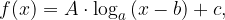
približuje premici, ki ji pravimo navpična asimptota, in ki je enaka koeficientu b:
Navpična asimptota:
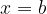
V primeru osnovne oblike, je koeficient b enak 0. Takrat je navpična asimptota funkcije ordinatna os.
Konstanta A in prosti člen c na navpično asimptoto ne vplivata.
Funkcija je injektivna, ker se vsak x preslika v natanko en y.
Funkcija je surjektivna, ker vsakemu y pripada vsaj en x, ki se vanj preslika.
Funkcija je bijektivna, saj je injektivna in surjektivna.
Pri določanju injektivnosti in surjektivnosti si lahko pomagamo tudi z vzporednicami abscisni osi. Več o tem lahko preberete v gradivu Funkcije in njene lastnosti.
Vsem grafom osnovne logaritemske funkcije je skupno presečišče z abscisno osjo (ničla funkcije), to je točka 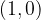 .
.
V primeru splošne oblike pa naš graf funkcije več ne poteka skozi točko 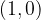 .
.
Logaritemska funkcija 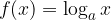 ni soda ker:
ni soda ker:
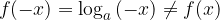
Logaritemska funkcija 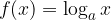 ni liha ker:
ni liha ker: