Osebne zbirke


V gradivu Električna poljska jakost smo se naučili, kako se računa sila na naboj v električnem polju. Imenovali smo jo električna sila. Zaradi te sile se naboj, ki sprva miruje, prične gibati enakomerno pospešeno v ravni črti - v smeri silnic električnega polja.
Električno nabit delec postavimo sedaj v magnetno polje trajnega magneta. Pričakovali bi, da tudi magnetno polje povzroči silo na električno nabiti delec in se bo delec pričel gibati. Delec pa še naprej miruje. Najprej pomislimo, da magnetna sila sploh ne deluje na naelektrene delce.
Sklep je le deloma pravilen. Magnetna sila je res enaka nič, če naboj miruje. Kaj pa če se giblje? V tem primeru obstaja tudi magnetna sila.
V tem gradivu se bomo naučili določiti:
velikost in smer magnetne sile na gibajoč, električno nabiti delec,
tir gibanja delca zaradi magnetne sile.
Spoznali bomo tudi nekaj naprav, ki delujejo na osnovi magnetne sile na gibajoče naelektrene delce:
Hallov element,
masni spektrometer,
krožni pospeševalnik ali ciklotron.
Električno nabit delec prileti v magnetnega polje. Hitrost delca 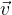 in smer polja
in smer polja 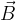 naj bosta pravokotna. Preden je priletel v magnetno polje, je bilo njegovo gibanje enakomerno in premočrtno. Po vstopu v magnetno polje prične na njega delovati magnetna sila.
naj bosta pravokotna. Preden je priletel v magnetno polje, je bilo njegovo gibanje enakomerno in premočrtno. Po vstopu v magnetno polje prične na njega delovati magnetna sila.
Poglejmo natančneje, kako določimo smer in velikost magnetne sile.
Magnetna sila deluje pravokotno na smer gibanja delcev. Smer magnetne sile lahko določimo na dva načina.
Pravilo desnega vijaka
Smer sile 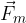 določimo kot smer premika desnega vijaka, če zavrtimo vektor hitrosti
določimo kot smer premika desnega vijaka, če zavrtimo vektor hitrosti 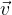 po najkrajši poti v vektor gostote magnetnega polja
po najkrajši poti v vektor gostote magnetnega polja 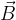 .
.
Pravilo leve roke
Smer sile lahko preprosto določimo tudi s pomočjo pravila leve roke, kot kaže slika. Iztegnjeni prsti so smer gibanja pozitivno nabitih delcev, silnice magnetnega polja grejo v dlan, iztegnjen palec kaže smer sile.
Krogec s križcem pri 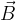 na gornji sliki pomeni, da je vektor
na gornji sliki pomeni, da je vektor 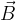 usmerjen stran od opazovalca - torej v zaslon.
usmerjen stran od opazovalca - torej v zaslon.
Če smer gibanja delca ni pravokotna na smer magnetnega polja, je magnetna sila vseeno pravokotna na hitrost delca. Vendar pa je velikost sile manjša (velikost magnetne sile se naučimo izračunati v nadaljevanju). Magnetno silo namreč povzroča le tista komponenta 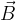 , ki je pravokotna na hitrost
, ki je pravokotna na hitrost 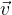 .
.
Poglejmo, kako izračunamo velikost magnetne sile.
S poskusi so ugotovili, da je velikost magnetne sile premo sorazmerna naboju in hitrosti delca. Faktor sorazmernosti pa je gostota magnetnega polja B:
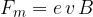
Če smeri hitrosti delca in magnetnega polja nista pravokotni, potem upoštevamo le:
velikost komponente 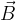 , ki je pravokotna na hitrost
, ki je pravokotna na hitrost 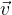 ali pa
ali pa
velikost tiste komponente vektorja hitrosti 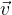 , ki je pravokotna na gostoto magnetnega polja
, ki je pravokotna na gostoto magnetnega polja 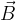 .
.
Velikost magnetne sile izračunamo po enačbi:
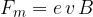
Magnetna sila je pravokotna na smer gibanja delca. Njeno smer določimo s pomočjo desnosučnega vijaka ali s pravilom leve roke.
Magnetna sila deluje pravokotno na smer gibanja delca in na delcu povzroči spremembo smeri gibanja. Delec sili v krožno gibanje. Ker ne deluje v smeri gibanja, delcu ne spreminja velikosti hitrosti. Spreminja samo smer hitrosti.
Spomnimo se na enakomerno kroženje. Silo, ki spreminja smer gibanja telesa in ga sili v krožnico, smo imenovali radialna sila 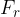 . Usmerjena je proti središču krožnice. Tudi delec, ki prileti s stalno hitrostjo v magnetno polje, bo zaradi magnetne sile zaokrožil. Magnetna sila je torej enaka radialni sili in povzroči enakomerno kroženje delca.
. Usmerjena je proti središču krožnice. Tudi delec, ki prileti s stalno hitrostjo v magnetno polje, bo zaradi magnetne sile zaokrožil. Magnetna sila je torej enaka radialni sili in povzroči enakomerno kroženje delca.
Narišimo sliko električno nabitega delca, ki se giblje pravokotno na silnice magnetnega polja po krožnem tiru:
Med kroženjem je rezultanta sil, ki delujejo na delec enaka radialni sili. Ker radialno silo povzroča magnetna sila, velja:
Delec, ki prileti pravokotno na silnice magnetnega polja s stalno hitrostjo v, v polju zaokroži. Pri tem velja, da je magnetna sila enaka radialni sili:
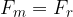
ali
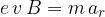
Oglejmo si naslednje naprave:
Hallov element,
masni spektrometer,
krožni pospeševalnik električno nabitih delcev.
Hallov element uporabljamo za:
ugotavljanje prisotnosti magnetnega polja (Hallov senzor ali tipalo),
meritev gostote magnetnega polja.
Hallov element je sestavljen iz ploščice - kvadra s štirimi priključnimi elektrodami. Običajno je narejen iz materiala, ki mu pravimo polprevodnik. To je npr. silicij ali germanij z dodanimi primesmi. Poenostavljeno si lahko predstavljamo, da primesi določajo, ali bodo v polprevodniku gibljivi nosilci naboja pozitivno ali negativno nabiti delci.
Na spodnji sliki je izbran polprevodnik s pozitivnimi gibljivimi nosilci naboja. Smer toka je v tem primeru enaka smeri gibanja naboja. Ploskve A, B, C in D so metalizirane, vendar se ne stikajo.
Med ploskvama A in B je priključena baterijska napetost 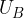 . Med ploskvama C in D, ki sta razmaknjeni za d, pa merimo Hallovo napetost
. Med ploskvama C in D, ki sta razmaknjeni za d, pa merimo Hallovo napetost 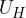 :
:
Če ni zunanjega magnetnega polja, se gibljejo nosilci naboja naravnost od ploskve A proti ploskvi B, kot kaže zgornja slika. Ploskvi C in D ostajata električno nevtralni, zato je Hallova napetost nič.
Zdaj damo ploščico v magnetno polje. Silnice magnetnega polja pravokotno prebadajo polprevodniško ploščico - spodnja slika. Tir gibanja pozitivnega naboja se zaradi magnetne sile ukrivil proti levi ploskvi C, zato plošča C prejme pozitivni naboj e. Plošča D pa se odzove tako, da se na njej nabere enako velik negativni naboj -e.
Med ploskvama nastane električno polje jakosti E. Ta deluje na gibajoči nabiti delec z električno silo, ki je nasprotna magnetni sili - spodnja slika levo.
Naboj na ploščah C in D se nabira toliko časa, dokler električna sila ne postane tako velika, da uravnovesi magnetno silo. Takrat sta električna in magnetna sila nasprotno enaki in je njuna rezultanta nič. Zato se bodo poslej nosilci naboja gibali naravnost proti ploskvi B - spodnja slika desno.
Iz pogoja za enakost obeh sil lahko izračunamo Hallovo napetost.
Hallova napetost je torej sorazmerna gostoti magnetnega polja B, hitrosti nosilcev naboja in razmika med ploščama. Pri znani hitrosti nosilcev in razmiku d lahko z meritvijo Hallove napetosti izračunamo gostoto magnetnega polja B.
To je naprava, ki omogoča analizo elementov, prisotnih v curku snovi. Elementi, iz katerih sestoji masni curek, morajo imeti na vhodu masnega spektrometra enako hitrost in enak naboj. Med sabo se lahko razlikujejo le po atomskih ali molekularnih masah.
Nabiti delci po vstopu v magnetno polje gostote B zaokrožijo. Radij kroženja je sorazmeren masi delca:
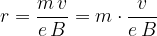
Po približno četrtini kroga zadenejo zaslon, kar povzroči na zaslonu svetlobno sled. Iz razmika točk na zaslonu (radijev kroženja) sklepamo, kateri kemijski elementi so prisotni v masnem curku.
Namenjen je pospeševanju električno nabitih delcev. Delci v pospeševalniku lahko dosežejo hitrosti, ki so blizu svetlobne hitrosti. Pospešeni delci lahko zadenejo in razbijajo molekule ali atome snovi in nam tako omogočajo vpogled v zgradbo snovi.
Uporabljajo se za:
raziskave na področju molekul in atomov,
za sintezo izotopov, namenjenih industriji in medicini.
V času pospeševanja se lahko delci gibljejo po ravnem tiru (linearni pospeševalniki) ali po krožnem tiru (krožni pospeševalniki). V tem gradivu si bomo ogledali krožni pospeševalnik, imenovan ciklotron.
Ciklotron ima dve votli elektrodi v obliki polvaljev. V preseku sta to modro šrafirani področji na spodnji sliki. Na njiju je priključena izmenična električna napetost, ki ustvarja v prostoru med obema polvaljema izmenično električno polje E. Izmenična napetost naj bo pravokotne oblike, da bo sila na delec med pospeševanjem stalna.
Znotraj polvaljev je magnetno polje z gostoto B, ki ga povzroča tuljava. Magnetno polje je usmerjeno tako, da se tir delcev v njem krivi.
V sredini ciklotrona je izvir električno nabitih delcev: elektronov, protonov ali ionov - glej sliko.
Predpostavimo, da pospešujemo pozitivno nabite delce, npr. protone. Delec se nahaja v središču ciklotrona. Električno polje je po zgornji sliki najprej usmerjeno v levo in protone pospeši. Njihovo hitrost ob vstopu v levi polvalj lahko izračunamo po enačbi:
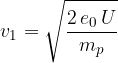
Proton v levem polvalju se na silnicah magnetnega polja zakrivi in zaokroži za polovico kroga. Radij prvega polkroga je:
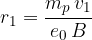
Ko delec preleti polovico kroga, se zamenja predznak izmenične napetosti tako, da se delec v prostoru med elektrodama ponovno pospešuje. Frekvenca izmenične napetosti mora biti zato enaka frekvenci kroženja delcev.
Po vsakem preletu reže med obema polvaljema se hitrost delcev poveča, poveča pa se jim tudi radij kroženja. Delec se giblje po spirali - rdeča krivulja na sliki. Na izhodu ciklotrona kroži po radiju r in doseže hitrost v.
Ali se obhodni čas in frekvenca kroženja kaj spreminjata, ko naraščata hitrost in radij kroženja? Izpeljimo enačbo za frekvenco kroženja!
Izenačimo magnetno in radialno silo:
Frekvenca kroženja in obhodni čas delca z maso m in nabojem e nista odvisni od trenutne hitrosti delca ali trenutnega radija kroženja, pač pa samo od gostote magnetnega polja B.
Prednost ciklotrona je, da lahko z razmeroma majhno napravo dosegamo velike hitrosti delcev. Pri pospeševanju protonov lahko dosegamo hitrosti delcev do desetine svetlobne hitrosti.