Osebne zbirke


V tem gradivu so opisani matematični simboli, ki se uporabljajo:
v teoriji množic in
v geometriji.
V teoriji množic z njimi opisujemo medsebojne odnose med množicami (npr. številskimi), v geometriji pa medsebojne odnose med geometrijskimi elementi (npr. med točko in premico).
V geometriji je vsak element sestavljen iz velikega števila osnovnih elementov - točk, kar pomeni, da je vsak geometrijski element množica. Zato tako za množice kot geometrijske elemente uporabljamo iste simbole.
Naj bosta A in B množici.
Če želimo z matematičnimi simboli zapisati, da sta množici A in B enaki, uporabimo enačaj:
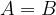
Če želimo z matematičnimi simboli zapisati, da množici A in B nista enaki, uporabimo neenačaj:
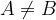
Naj bosta p in q premici.
Če želimo z matematičnimi simboli zapisati, da premici p in q sovpadata, uporabimo enačaj:
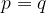
Če želimo z matematičnimi simboli zapisati, da premici p in q ne sovpadata, uporabimo neenačaj:
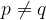
Naj bo A množica, x pa element množice.
Če želimo z matematičnimi simboli zapisati, da je x element množice A, uporabimo simbol "je element":
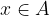
Če želimo z matematičnimi simboli zapisati, da x ni element množice A, uporabimo simbol "ni element":
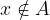
Naj bo A točka, p pa premica.
Če želimo z matematičnimi simboli zapisati, da točka A leži na premici p, uporabimo simbol "je element":
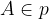
Če želimo z matematičnimi simboli zapisati, da točka A ne leži na premici p, uporabimo simbol "ni element":
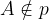
Naj bodo A, B in C množice:
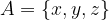
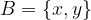
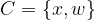
B je podmnožica množice A, saj se oba elementa množice B nahajata tudi v množici A.
Če želimo z matematičnimi simboli zapisati, da je B podmnožica množice A, uporabimo simbol "je podmnožica":
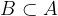
C ni podmnožica množice A, saj se le element x nahaja tudi v množici A, element w pa ne.
Če želimo z matematičnimi simboli zapisati, da C ni podmnožica množice A,uporabimo simbol "ni podmnožica":
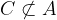
Naj bo p premica, AB pa daljica.
Če želimo z matematičnimi simboli zapisati, da daljica AB leži na premici p, uporabimo simbol "je podmnožica":
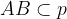
Če želimo z matematičnimi simboli zapisati, da daljica AB ne leži na premici p, uporabimo simbol "ni podmnožica":
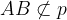
Naj bosta A in B množici:
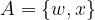
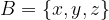
Element x predstavlja presek množic A in B, če se nahaja hkrati v množici A in v množici B.
Če želimo z matematičnimi simboli zapisati, da element x predstavlja presek množic A in B, uporabimo simbol "je presek":
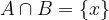
Naj bosta r in s premici, ki se sekata v točki T:
Če želimo z matematičnimi simboli zapisati, da točka T predstavlja presečišče premic r in s, uporabimo simbol "je presek":
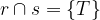
Naj bosta A in B množici:
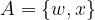
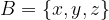
Unijo množic A in B predstavljajo elementi, ki se nahajajo bodisi v prvi, bodisi v drugi ali v obeh množicah.
Če želimo z matematičnimi simboli zapisati, da se elementi w, x, y in z nahajajo vsaj v eni od podanih množic (A ali B), uporabimo simbol "je unija":
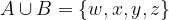
Naj bo p premica, na kateri ležijo točke A, B in C:
Daljica AC predstavlja unijo daljic AB in BC, saj vsebuje vse točke tako daljice AB kot daljice BC.
Če želimo z matematičnimi simboli zapisati, da daljica AC vsebuje vse točke daljice AB in vse točke daljice BC, uporabimo simbol "je unija":