Osebne zbirke


Matematično ali nitno nihalo je teoretično nihalo, saj predpostavlja, da je teža vrvice, na kateri niha masna točka, enaka nič. Rezultati izračunov frekvence nihanja veljajo približno tudi za realna nihala, kjer niha
dimenzijsko majhna masa;
na niti z maso mnogo manjšo od uteži;
z majhno amplitudo.
Na lahki vrvici imamo obešeno utež. Izmaknemo jo iz ravnovesne lege za temenski odmik in ji damo potencialno energijo. Ko utež spustimo, se le-ta pretvori v kinetično energijo in nato ponovno v potencialno energijo. Utež zaniha okoli ravnovesne lege, to je točke v najnižji legi nihanja.
Matematično nihalo je približno harmonično (sinusno) nihalo samo za majhne amplitude nihanja, kar bomo pokazali pri izpeljavi frekvence nihanja.
Izračunajmo frekvenco in nihajni čas opisanega nihala:
Pri temenskem odmiku 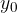 deluje na maso
deluje na maso 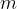 sila, ki je nasprotno usmerjena od prvotnega gibanja in je zato negativna:
sila, ki je nasprotno usmerjena od prvotnega gibanja in je zato negativna:
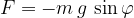
oziroma pospešek:

Temenski odmik 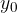 od ravnovesne lege je lok krožnice s polmerom
od ravnovesne lege je lok krožnice s polmerom 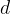 in kotom
in kotom 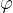 :
:
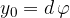
Obrnimo enačbo tako, da dobimo 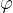 :
:
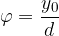
Vstavimo to v enačbo (2):
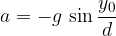
Spomnimo se, da je pri harmoničnem nihanju pospešek sorazmeren temenskemu odmiku od ravnovesne lege:
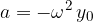
in ne njegovi sinusni vrednosti.
V našem primeru bo približno sorazmeren le pri majhnih kotih, ko je sinus kota enak kotu:
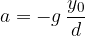
Izenačimo desni strani zadnjih dveh enačb in dobimo:
Frekvenca 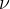 je:
je:
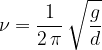
in nihajni čas 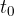 :
:
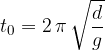
V enačbi za nihajni čas je dolžina niti in gravitacijski pospešek, ni pa mase. To pa ne pomeni, da bi nihalo nihalo tudi brez mase, kajti v tem primeru tudi ne bi bilo sile teže, ki omogoča nihanje.
Nitno nihalo ima krožno frekvenco:
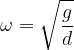
frekvenco:
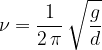
in nihajni čas: