Osebne zbirke


Količina je neka lastnost, ki jo lahko izmerimo ali pa preštejemo. Z njo opišemo telesa, snovi ali dogodke in podobno.
Količine merimo z enotami. S pomočjo enot količine med seboj primerjamo in opazujemo, kako se spreminjajo.
Količine so lahko med seboj odvisne ali neodvisne. Če sprememba ene količine vpliva na spremembo druge, sta količini odvisni.
Ko sta količini odvisni, eno izmed njiju lahko poljubno izberemo ali spremenimo. Imenujemo jo neodvisna spremenljivka.
Druga količina pa se prilagaja prvi in je ne moremo poljubno izbirati, zato jo imenujemo odvisna spremenljivka.
Odvisnosti količin lahko zapišemo matematično, v obliki enačbe ali formule.
Vsaka enačba vsebuje odvisno in neodvisno spremenljivko, dodatno pa so v njej lahko tudi številske vrednosti. Številske vrednosti v enačbah se ne spreminjajo, zato jih imenujemo konstante.
S pomočjo enačbe lahko izračunamo vrednost odvisne spremenljivke za poljubno vrednost neodvisne spremenljivke.
Če vrednost odvisne spremenljivke izračunamo za več vrednosti neodvisne spremenljivke, jih lahko uredimo v obliki tabele:
v prvem stolpcu tabele navedemo vrednosti neodvisne spremenljivke (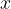 ),
),
v drugem pa vrednosti odvisne spremenljivke (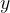 ).
).
Tabelo uredimo tako, da sta vrednost 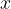 in njej pripadajoča vrednost
in njej pripadajoča vrednost 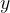 ena poleg druge.
ena poleg druge.
Koordinatna mreža je sestavljena iz vodoravne in navpične osi:
vodoravno os označimo z 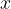 in jo imenujemo os
in jo imenujemo os 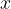 ali abscisna os,
ali abscisna os,
navpično os označimo z 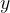 in jo imenujemo os
in jo imenujemo os 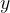 ali ordinatna os.
ali ordinatna os.
Na os 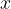 nanašamo vrednosti neodvisnih količin. Na os
nanašamo vrednosti neodvisnih količin. Na os 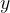 pa nanašamo vrednosti odvisnih količin.
pa nanašamo vrednosti odvisnih količin.
V koordinatni mreži lahko narišemo točko in položaj točke je s tem natanko določen.
Vsaka točka na koordinatni mreži je določena z dvema številoma, ki ju imenujemo koordinati. Koordinate vedno zapišemo v obliki urejenega para 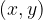 , kjer je prva vrednost koordinata
, kjer je prva vrednost koordinata 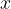 , druga pa koordinata
, druga pa koordinata 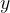 na navpični osi.
na navpični osi.
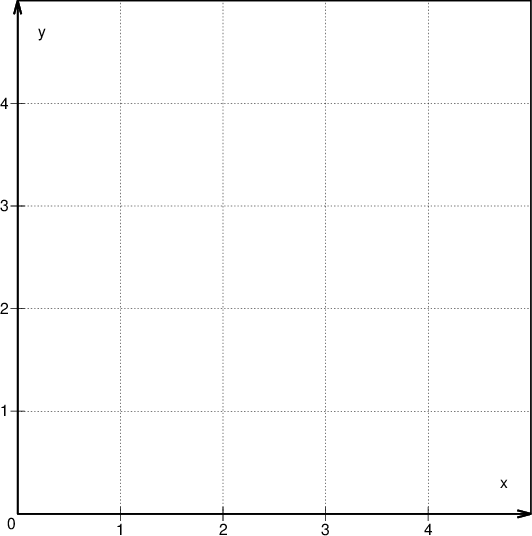
Točke v koordinatni mreži narišemo na naslednji način:
Najprej določimo merila osi,
nato poiščemo vrednost prve koordinate 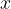 na vodoravni osi,
na vodoravni osi,
nato poiščemo vrednost druge koordinate 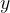 na navpični osi,
na navpični osi,
točko označimo na presečišču teh dveh vrednosti.
Pri risanju ali branju točk pazimo na izbiro ustreznega merila obeh osi, saj s tem zagotovimo, da so točke dobro razporejene in jih lahko natančno odčitamo.
Merilo na oseh je dobro izbrati tako, da so koordinate točk usklajene z merilom. To pomeni:
če so vrednosti 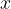 in
in 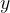 majhna naravna števila, potem na merilu izberemo enoto 1,
majhna naravna števila, potem na merilu izberemo enoto 1,
če so vrednosti 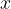 in
in 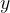 večja naravna števila, potem na merilu zapišemo večja števila, na primer 10, 20, 30 ... ali 100, 200, 300 ...
večja naravna števila, potem na merilu zapišemo večja števila, na primer 10, 20, 30 ... ali 100, 200, 300 ...
Če imamo v mreži že označeno točko, potem njene koordinate odčitamo na naslednji način:
Najprej odčitamo vrednost, ki ustreza točki na osi 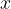 ,
,
nato odčitamo vrednost, ki ustreza točki na osi 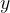 .
.
Če neodvisne spremenljivke in njim pripadajoče vrednosti odvisnih spremenljivk zapišemo kot urejene pare (točke) in jih prikažemo v koordinatnem sistemu, dobimo graf. Graf je skupek točk v koordinatni mreži in prikazuje, kako se vrednosti ene spremenljivke spreminjajo v odvisnosti od druge.
Glede na vrsto podatkov lahko odvisnost spremenljivk prikažemo v obliki točkovnega ali črtnega prikaza.
Točkovni prikaz uporabimo, kadar lahko za neodvisno spremenljivko izberemo samo nekaj določenih vrednosti, saj vmesne vrednosti ne obstajajo. Primer take neodvisne spremenljivke so dnevi v tednu.
Med točkami v mreži, ki pripadajo dnevom, ni dodatnih točk. Zato točke na grafu med seboj niso povezane s črto.
Črtni prikaz uporabimo, ko prikazujemo povezane količine, kjer med točkami poteka neprekinjena sprememba vrednosti.
Točke na grafu med seboj povežemo z ravnimi črtami.
Če ob povečanju vrednosti ene spremenljivke druga narašča, gre za naraščajočo odvisnost. Če pa ob povečanju prve vrednosti druga pada, gre za padajočo odvisnost.
Poleg besedilnega opisa si lahko pomagamo tudi z grafom.
Pri naraščajoči odvisnosti se graf vzpenja navzgor od leve proti desni: ko vrednosti na vodoravni osi (neodvisna spremenljivka) naraščajo, vrednosti na navpični osi (odvisna spremenljivka) prav tako naraščajo.
Pri padajoči odvisnosti graf poteka navzdol od leve proti desni: ko vrednosti na vodoravni osi (neodvisna spremenljivka) naraščajo, vrednosti na navpični osi (odvisna spremenljivka) padajo.