Osebne zbirke


Metodo bisekcije uporabljamo pri funkcijah, katerih ničle ne moremo neposredno preračunat, lahko pa poiščemo poljubno majhen interval, na katerem se ničla nahaja. Predpostavka za iskanje ničel z metodo bisekcije je, da na intervalu [a,b] funkcija menja predznak. V tem primeru je na tem intervalu vsaj ena ničla.
Naj bo dan polinom f(x). Na intervalu [a,b] je vsaj ena ničla, če velja
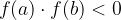
Interval, na katerem naš polinom menja predznak, razpolovimo in pogledamo predznak funkcije v novi točki. Nova točka nadomesti tisto staro točko, s katero imata enak predznak. Nadaljujemo z razpolavljanje intervalov, dokler nismo zadovoljni z rezultatom.
Poglejmo, kako metoda deluje na praktičnem primeru.